Geometric algebra and classical mechanics

Date: 2015-10-07; view: 526.

It is now straightforward to use the formalism described so far in classical mechanics as was done in [3]. We will here only give two examples to show where the advantages of geometric algebra lie. Let us first consider the three-dimensional harmonic oscillator, which is defined by the differential equation 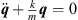, where q is now a supernumber: q = q₁σ₁ + q₂σ₂ + q₃σ₃. The ansatz leads to the equation , which is solved by λ = ± iω₀ with . The difference to the conventional formalism is that i is here a bivector with . This gives then the two solutions

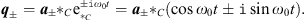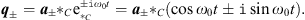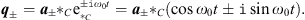
(4.1)

In the second term appears the expression a_{± C}i = a_±i + a_± · i, which is the sum of a term of Grassmann grade three and a term of Grassmann grade one. But the result q_± itself is a quantity of Grassmann grade one, so it follows that a_±i = 0, which is the defining equation of the plane in which the oscillatory movement takes place. This plane is defined by the unit bivector i and has to be determined by the initial conditions [3].

As the second example we consider the solution of the Kepler problem by spinors [11]. One uses here the fact that the radial position vector r = r₁σ₁ + r₂σ₂ + r₃σ₃ can be written as a rotated and dilated basis vector:

(4.2)

The components r_i of r can then be expressed in terms of the components u_i of U = u₁ + u₂σ₂σ₃ + u₃σ₃ σ₁ + u₄σ₁σ₂:

(4.3)

which is the well-known Kustaanheimo–Stiefel transformation [12] and [13]. Comparing Figs. (4.2) and (4.3) leads to the notational correspondence

(4.4)

where and are four-dimensional space vectors considered as tupels of numbers as in the conventional formalism. One should note here that the KS-transformation increases the degrees of freedom by one, which means that the bivector U in (4.2) is not unique [11]. This gauge freedom can be reduced by imposing an additional constraint on U as will be shown below. Squaring (4.4) leads to the relations

(4.5)

with . Differentiating (4.4) with respect to t one obtains the KS-transformation for the velocities as

(4.6)

One can then choose for the constraint

(4.7)

which means that the superfluous fourth component r₄ stays zero for all times. With this constraint it is possible to invert the geometric algebra relation (4.6) for U. Implementing Figs. (4.7) and (4.6) gives , which can be solved for , so that the inverse relation to (4.6) is

(4.8)

By introducing a fictitious time s which is defined as

(4.9)

it is then possible to regularize the divergent 1/r-potential so that (4.8) reads 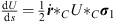or

(4.10)

Substituting now the inverse square force

(4.11)

one obtains:

(4.12)

which is the equation of motion for an harmonic oscillator. This equation can be solved in a straightforward fashion and is much easier than the equation for r. The orbit can then be calculated by (4.2).

The Kepler problem can also be treated in the canonical formalism. For this purpose one first needs the KS-transformation for the momentum. If is the canonical momentum corresponding to the KS-transformation is given by

(4.13)

with W = w₁ + w₂σ₂σ₃ + w₃σ₃σ₁ + w₄σ₁σ₂. For one gets with (4.13)

(4.14)

where and

(4.15)

Equation (4.14) allows to transform the Hamiltonian into u_i- and w_i-coordinates. This is done in several steps [13]. Starting from the Hamiltonian one first extends the phase space by a q₀- and a p₀-coordinate and forms the homogenous Hamiltonian as H₁ = H + p₀. This leads for the zero component to two additional Hamilton equations

(4.16)

which shows that q₀ corresponds to the time t and p₀ is a constant and corresponds to the negative energy of the system, so that H₁ = H + p₀ = 0 for a conservative force. Since the time is now a coordinate the development of the system has to be described with a different parameter. This development parameter is the fictitious time s that is connected to the time by (4.9). The relation (4.9) can be implemented if one chooses H₂ = rH₁. The Hamilton equations that describe then the development according to s are differential equations with respect to s:

(4.17)

Especially for the zero component one gets

which corresponds to (4.9). After having so far regularized the Hamiltonian one can then go over to KS-coordinates and obtains with (4.14)

(4.18)

Imposing now the constraint p₄ = 0, which for in (4.15) is just (4.7), and considering bound states with E < 0 the Hamiltonian is given by

(4.19)

which describes a four-dimensional harmonic oscillator with fixed energy and frequency ω = (|E|/2m)^1/2.

The formalism of geometric algebra can also be applied to hamiltonian mechanics [14]. The 2d-dimensional phase space is then spanned by d basis elements {η_i} for the space coordinates and d basis elements {ρ_i} for the momentum coordinates so that a point in phase space is described by the vector 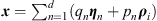and the Clifford star product on the phase space has the from

(4.20)

so that η_m · η_n = ρ_m · ρ_n = δ_mn and η_m · ρ_n = 0. The two d-dimensional subspaces are related by a bivector j, which is the generalization of the imaginary structure in two dimensions and is defined as:

(4.21)

This bivector plays the role of the symplectic form that relates the space and momentum part of the phase space according to

(4.22)

In phase space one has then two possibilities to assign a scalar to two phase space vectors a and b, apart from the scalar product a · b one can also form the expression

(4.23)

With the gradient operator

(4.24)

the Hamilton equation can for example be written as:

(4.25)

or explicitly:

(4.26)

With (4.25) one gets for the time derivation of a scalar phase space function f (x):

(4.27)

The Poisson bracket can be written in a compact way as:

(4.28)