
Geometric algebra and the Clifford star product
Date: 2015-10-07; view: 670.
Starting point for geometric algebra [1] and [3] is an n-dimensional vector space over the real numbers with vectors a,b,c, … A multiplication, called geometric product, of vectors can then be denoted by juxtaposition of an indeterminate number of vectors so that one gets monomials A, B, C, … These monomials can be added in a commutative and associative manner: A + B = B + A and (A + B) + C = A + (B + C), so that they form polynomials also denoted by capital letters. The so obtained polynomials can be multiplied associatively, i.e., A (BC) = (AB) C and they fulfill the distributive laws (A + B) C = AC + BC and C (A + B) = CA + CB. Furthermore, there exists a null vector a0 = 0 and the multiplication with a scalar λa = aλ, with  . The connection between scalars and vectors can be given if one assumes that the product ab is a scalar iff a and b are collinear, so that
. The connection between scalars and vectors can be given if one assumes that the product ab is a scalar iff a and b are collinear, so that  is the length of the vector a. These axioms define now the Clifford algebra Cℓ (V) and the elements A, B, C, … of Cℓ (V) are called Clifford or c-numbers.
is the length of the vector a. These axioms define now the Clifford algebra Cℓ (V) and the elements A, B, C, … of Cℓ (V) are called Clifford or c-numbers.
Since the geometric product of two collinear vectors is a scalar, the symmetric part of the geometric product  is a scalar denoted
is a scalar denoted  . The product a · b is the inner or scalar product. One can then decompose the geometric product into its symmetric and antisymmetric part:
. The product a · b is the inner or scalar product. One can then decompose the geometric product into its symmetric and antisymmetric part:

| (3.1) |
where the antisymmetric part  is formed with the outer product. For the outer product one has obviously a
is formed with the outer product. For the outer product one has obviously a  b = −b
b = −b  a and a
a and a  a = 0, so that a
a = 0, so that a  b can be interpreted geometrically as an oriented area. The geometric product is constructed in such a way that it gives information over the relative directions of a and b, i.e., ab = ba = a · b
b can be interpreted geometrically as an oriented area. The geometric product is constructed in such a way that it gives information over the relative directions of a and b, i.e., ab = ba = a · b  a
a  b = 0 means that a and b are collinear whereas ab = −ba = a
b = 0 means that a and b are collinear whereas ab = −ba = a  b
b  a · b = 0 means that a and b are perpendicular.
a · b = 0 means that a and b are perpendicular.
With the outer product one defines simple r-vectors or r-blades
Ar=a1  a2 a2    ar, ar,
| (3.2) |
which can be interpreted as r-dimensional volume forms. The geometric product can then be generalized to the case of a vector and an r-blade:
aAr=a·Ar+a  Ar, Ar,
| (3.3) |
which is the sum of an (r−1)-blade  and a (r + 1)-blade
and a (r + 1)-blade 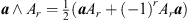 . Applying this recursively one sees that each c-number can be written as a polynomial of r-blades, and using a set of basis vectors e1, e2, … , er a c-number reads:
. Applying this recursively one sees that each c-number can be written as a polynomial of r-blades, and using a set of basis vectors e1, e2, … , er a c-number reads:

| (3.4) |
A is called a multivector or r-vector if the highest appearing grade is r. It decomposes into several blades:

| (3.5) |
where 
 n projects onto the term of grade n. A multivector Ar is called homogeneous if all appearing blades have the same grade, i.e., Ar =
n projects onto the term of grade n. A multivector Ar is called homogeneous if all appearing blades have the same grade, i.e., Ar =  Ar
Ar  r. The geometric product of two homogeneous multivectors Ar and Bs can be written as
r. The geometric product of two homogeneous multivectors Ar and Bs can be written as
ArBs=  ArBs ArBs  r+s+ r+s+  ArBs ArBs  r+s-2+ r+s-2+  + +  ArBs ArBs  |r-s|. |r-s|.
| (3.6) |
The inner and the outer product stand now for the terms with the lowest and the highest grade:

| (3.7) |
One should note that the inner and outer product here in the general case do not correspond anymore to the symmetric and the antisymmetric part of the geometric product. For example, in the case of two bivectors one has A2  B2 = B2
B2 = B2  A2, so that the outer product is symmetric. Actually one finds for the symmetric and the antisymmetric parts of A2B2:
A2, so that the outer product is symmetric. Actually one finds for the symmetric and the antisymmetric parts of A2B2:

| (3.8) |
In general the commutativity of the outer and the inner product is given by:

| (3.9) |
and both products are always distributive:

| (3.10) |
Only the outer product of r-vectors is in general associative, i.e., A  (B
(B  C) = (A
C) = (A  B)
B)  C, for the inner product one gets:
C, for the inner product one gets:

| (3.11) |
If one has to calculate several products of different type, the inner and the outer product always have to be calculated first, i.e.,

| (3.12) |
The formalism of geometric algebra briefly sketched so far can now be described with Grassmann variables and the Clifford star product, that turns the Grassmann algebra into a Clifford algebra. To make the equivalence even more obvious we go over to the dimensionless Grassmann variables
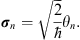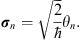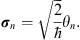
| (3.13) |
These variables play here the role of dimensionless basis vectors and will therefore be written in bold face, whereas the θi played in the discussion of the first section the role of dynamical variables with dimension 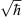 . In the σn-variables the Clifford star product (2.12) has the form
. In the σn-variables the Clifford star product (2.12) has the form

| (3.14) |
As a star product the Clifford star product is associative and distributive.
To show how the geometric algebra described with Grassmann variables and the Clifford star product looks like, we first consider the two-dimensional euclidian case. One has then two Grassmann basis elements σ1 and σ2, so that a general element of the Clifford algebra is a supernumber A = a0 + a1σ1 + a2σ2 + a12σ1 σ2 =  A
A  0 +
0 +  A
A  1 +
1 +  A
A  2 and a vector corresponds to a supernumber with Grassmann grade one: a = a1σ1 + a2σ2. The Clifford star product of two of these supernumbers is
2 and a vector corresponds to a supernumber with Grassmann grade one: a = a1σ1 + a2σ2. The Clifford star product of two of these supernumbers is

| (3.15) |
where the symmetric and the antisymmetric part of the Clifford star product is given by:

| (3.16) |
and

| (3.17) |
which are terms with Grassmann grade 0 and 2, respectively. Note that now a juxtaposition like ab is just as in the notation of superanalysis the product of supernumbers and not the Clifford product, which we want to describe explicitly with the star product (3.14). The σi form an orthogonal basis under the scalar product:  .
.
The unit 2-blade i = σ1σ2 can be interpreted as the generator of 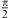 -rotations because by multiplying from the right one gets
-rotations because by multiplying from the right one gets

| (3.18) |
so that a vector x = x1σ1 + x2σ2 is transformed into  . The relation
. The relation  describes then a reflection and furthermore one has with (2.16):
describes then a reflection and furthermore one has with (2.16):  , so that i corresponds to the imaginary unit. The connection between the two-dimensional vector space with vectors x and the Gauss plane with complex numbers z is established by star multiplying x with σ1:
, so that i corresponds to the imaginary unit. The connection between the two-dimensional vector space with vectors x and the Gauss plane with complex numbers z is established by star multiplying x with σ1:

| (3.19) |
Such a bivector that results from star multiplying two vectors is also called spinor. While the bivector i generates a rotation of  when acting from the right, the spinor z generates a general combination of a rotation and dilation when acting from the right. One can see this by writing
when acting from the right, the spinor z generates a general combination of a rotation and dilation when acting from the right. One can see this by writing  with
with  . Acting from the right with z causes then a dilation by |z| and a rotation by
. Acting from the right with z causes then a dilation by |z| and a rotation by 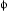 , one has for example: σ1
, one has for example: σ1  Cz=x, which is the inversion of (3.19). Here one can see that the formalism of geometric algebra reproduces complex analysis and gives it a geometric meaning.
Cz=x, which is the inversion of (3.19). Here one can see that the formalism of geometric algebra reproduces complex analysis and gives it a geometric meaning.
After having described the geometric algebra of the euclidian 2-space we now turn to the euclidian 3-space with basis vectors σ1, σ2, and σ3 and with the Clifford star product (3.14) for d = 3. The basis vectors are orthogonal: σi · σj = δij and a general c-number written as a supernumber has the form
| A=a0+a1σ1+a2σ2+a3σ3+a12σ1σ2+a13σ3σ1+a23σ2σ3+a123σ1σ2σ3. | (3.20) |
This multivector has now four different simple multivector parts. Besides the scalar part a0 there is the pseudoscalar part corresponding to I3 = σ1σ2σ3, which can be interpreted as a right handed volume form, because a parity operation gives (−σ1) (−σ2) (−σ3) = −I3. Moreover I3 has also the properties of an imaginary unit: 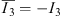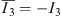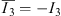 and I3
and I3  CI3 = I3 · I3 = −1. While the pseudoscalar I3 is an oriented volume element the bivector part with the basic 2-blades
CI3 = I3 · I3 = −1. While the pseudoscalar I3 is an oriented volume element the bivector part with the basic 2-blades

| (3.21) |
describes oriented area elements. Each of the ir plays in the plane it defines the same role as the i of the two-dimensional euclidian plane defined above. Star-multiplying with the pseudoscalar I3 is equivalent to taking the Hodge dual, for example to each bivector B = b1i1 + b2i2 + b3i3 corresponds a vector b = b1σ1 + b2σ2 + b3σ3, which can be expressed by the equation B = I3  Cb. This duality can for example be used to write the geometric product of two vectors a = a1σ1 + a2σ2 + a3σ3 and b = b1σ1 + b2σ2 + b3σ3 as:
Cb. This duality can for example be used to write the geometric product of two vectors a = a1σ1 + a2σ2 + a3σ3 and b = b1σ1 + b2σ2 + b3σ3 as:
a  Cb=a·b+I3 Cb=a·b+I3  C(a×b), C(a×b),
| (3.22) |
where  and a×b=εklmakblσm. Furthermore one finds:
and a×b=εklmakblσm. Furthermore one finds:
σ1×σ2=-I3  Cσ1 Cσ1  Cσ2=-I3 Cσ2=-I3  Cσ1σ2=σ3 Cσ1σ2=σ3
| (3.23) |
and cyclic permutations. Note also that one gets with the nabla operator  x=σ1∂x1+σ2∂x2+σ3∂x3 for the gradient of a vector field f = f1 (x1, x2, x3) σ1 + f2 (x1, x2, x3) σ2 + f3 (x1, x2, x3) σ3:
x=σ1∂x1+σ2∂x2+σ3∂x3 for the gradient of a vector field f = f1 (x1, x2, x3) σ1 + f2 (x1, x2, x3) σ2 + f3 (x1, x2, x3) σ3:
 x x  Cf= Cf= 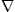 x·f+ x·f+ 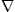 x x  f=divf+I3 f=divf+I3  Crotf. Crotf.
| (3.24) |
The multivector part of (3.20) with even Grassmann grade have the basis 1, i1, i2, i3 and form a closed subalgebra under the Clifford star product, namely the quaternion algebra. The multivector part of (3.20) with odd grade does not close under the Clifford star product, but nevertheless one can reinvestigate the definition of the Pauli functions in (2.14). Replacing in (2.14) the scalar i by the pseudoscalar I3 one sees that the basis vectors σi fulfill

| (3.25) |
which justifies denoting them σi. With the pseudoscalar I3 the trace (2.18) can be written as Tr (F) = 2∫dσ3 dσ2dσ1  F = 2∫dσ3 dσ2 dσ1I3
F = 2∫dσ3 dσ2 dσ1I3  CF. So one has here achieved with the Clifford star product a cliffordization of the three-dimensional Grassmann algebra of the σi.
CF. So one has here achieved with the Clifford star product a cliffordization of the three-dimensional Grassmann algebra of the σi.
Just as in the two-dimensional case one can also consider in three dimensions the role of spinors and rotations. To this purpose one first considers a vector transformation of the form
x→x′=-u  Cx Cx  Cu, Cu,
| (3.26) |
where u is a three-dimensional unit vector: u = u1σ1 + u2σ2 + u3σ3 with  . This transformation can be identified as a reflection in a plane orthogonal to u if one decomposes x into a part collinear to u and a part orthogonal to u:
. This transformation can be identified as a reflection in a plane orthogonal to u if one decomposes x into a part collinear to u and a part orthogonal to u:
x=x  +x +x  =(x·u+xu) =(x·u+xu)  Cu, Cu,
| (3.27) |
with x  = (x · u) u and x
= (x · u) u and x  = (xu)
= (xu)  Cu = (xu) · u. One can easily check that
Cu = (xu) · u. One can easily check that

| (3.28) |
This decomposition of x can most easily be obtained if one just star-divides x  Cu = x · u + x
Cu = x · u + x  u by u, which gives with u-1
u by u, which gives with u-1  C=u:
C=u:
x=(x·u)  Cu-1 Cu-1  C+(xu) C+(xu)  Cu-1 Cu-1  C=(x·u)u+(xu) C=(x·u)u+(xu)  Cu=x Cu=x  +x +x  . .
| (3.29) |
Using (3.28) one sees that the transformation (3.26) turns x into x′=-u  Cx
Cx  Cu=-x
Cu=-x  +x
+x  , so that only the component collinear to u is inverted, which amounts to a reflection at the plane where u is the normal vector. Two successive transformations (3.26) lead to:
, so that only the component collinear to u is inverted, which amounts to a reflection at the plane where u is the normal vector. Two successive transformations (3.26) lead to:

| (3.30) |
where U can be written as:

| (3.31) |
where the angle between the unit vectors u and v is described by an bivector A = v  u = vu = |vu|A0. Hereby the unit bivector A0 = vu/|vu| defines the plane in which the angle lies, while the magnitude |vu| gives the angle in radians, furthermore it fulfills A0
u = vu = |vu|A0. Hereby the unit bivector A0 = vu/|vu| defines the plane in which the angle lies, while the magnitude |vu| gives the angle in radians, furthermore it fulfills A0  CA0 = −1. If one chooses for example the basis vectors σk for u and v, A0 would be given by one of the bivectors in (3.21). The additional factor 1/2 in (3.31) will become clear if one investigates the action of the transformation (3.30). To this purpose one proceeds analogously to the discussion of the reflection (3.26). One first decomposes the vector x into a part x
CA0 = −1. If one chooses for example the basis vectors σk for u and v, A0 would be given by one of the bivectors in (3.21). The additional factor 1/2 in (3.31) will become clear if one investigates the action of the transformation (3.30). To this purpose one proceeds analogously to the discussion of the reflection (3.26). One first decomposes the vector x into a part x  in the plane defined by A and a part x
in the plane defined by A and a part x  perpendicular to that plane. This is done analogously to (3.29) by star-dividing x
perpendicular to that plane. This is done analogously to (3.29) by star-dividing x  CA = x · A + x
CA = x · A + x  A by A which leads to
A by A which leads to
x=(x·A)  CA-1 CA-1  C+(xA) C+(xA)  CA-1 CA-1  C=x C=x  +x +x  , ,
| (3.32) |
with x 
 C A = −A
C A = −A  Cx
Cx  and x
and x 
 CA = A
CA = A  Cx
Cx  . We then have for the transformation (3.30):
. We then have for the transformation (3.30):

| (3.33) |
So the component perpendicular to the plane defined by A is not changed while the component in this plane is rotated with the help of the spinor  by an angle of magnitude |A|, just as described in the two-dimensional case above. One sees here why the rotation in the two-dimensional case could be written just by acting with a spinor from the right. This is due to the fact that when the vector lies in the plane of rotation one has
by an angle of magnitude |A|, just as described in the two-dimensional case above. One sees here why the rotation in the two-dimensional case could be written just by acting with a spinor from the right. This is due to the fact that when the vector lies in the plane of rotation one has

| (3.34) |
A rotation can be described with the bivector A, but also with the dual vector a defined by A = I3  Ca, where the direction of a defines the axis of rotation, while the magnitude gives the radian |a| = |A|. So U can also be written as:
Ca, where the direction of a defines the axis of rotation, while the magnitude gives the radian |a| = |A|. So U can also be written as:

| (3.35) |
which corresponds to the star exponential (2.24).
The formalism described so far can easily be generalized to the case of d euclidian dimensions. Just as there is a duality in the space spanned by the σi there is also the duality between the spaces spanned by the σi and the σi. This duality is expressed by the relation  . The σi-vectors can be constructed with the help of the pseudoscalar, which is for the d-dimensional euclidian case Id = σ1σ2
. The σi-vectors can be constructed with the help of the pseudoscalar, which is for the d-dimensional euclidian case Id = σ1σ2  σd. The hyperplane for which the basis vector σj is normal is given for an d-dimensional euclidian space by the (d−1)-blade
σd. The hyperplane for which the basis vector σj is normal is given for an d-dimensional euclidian space by the (d−1)-blade 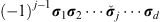 , where
, where  means that this basis vector is missing. The corresponding dual vector is then given by
means that this basis vector is missing. The corresponding dual vector is then given by

| (3.36) |
where  is the inverse d-dimensional pseudoscalar.
is the inverse d-dimensional pseudoscalar.
Note also that the multiple Clifford star product leads to an expansion of Wick type. For example, the Clifford product of four basis vectors is given by
σi1  Cσi2 Cσi2  Cσi3 Cσi3  Cσi4=σi1σi2σi3σi4+σi1σi2δi3i4-σi1σi3δi2i4+σi1σi4δi2i3+σi2σi3δi1i4-σi2σi4δi1i3+σi3σi4δi1i2+δi1i2δi3i4-δi1i3δi2i4+δi1i4δi2i3, Cσi4=σi1σi2σi3σi4+σi1σi2δi3i4-σi1σi3δi2i4+σi1σi4δi2i3+σi2σi3δi1i4-σi2σi4δi1i3+σi3σi4δi1i2+δi1i2δi3i4-δi1i3δi2i4+δi1i4δi2i3,
| (3.37) |
where the contraction of σi and σj is given by δij. This suggests to use the star product formalism also in the realm of quantum field theory [10].
| <== previous lecture | | | next lecture ==> |
| The star product formalism | | | Geometric algebra and classical mechanics |