
Exploration process
Date: 2015-10-07; view: 556.
An important property of the ensemble of curves γ on the lattice is that, instead of generating a configuration of all the s (R) and then identifying the curve, it may be constructed step-by-step as follows (see Fig. 2). Starting from r1, at the next step it should turn R or L according to whether the spin in front of it is +1 or −1. For independent percolation, the probability of either event is 1/2, but for x < 1 it depends on the values of the spins on the boundary. Proceeding like this, the curve will grow, with all the dual sites on its immediate left taking the value +1, and those its right the value −1. The relative probabilities of the path turning R or L at a given step depend on the expectation value of the spin on the site R immediately in front of it, given the values of the spins already determined, that is, given the path up to that point. Thus, the relative probabilities that the path turns R or L are completely determined by the domain and the path up to that point. This implies the crucial.
Property 2.1 Lattice version
Let γ1 be the part of the total path covered after a certain number of steps. Then the conditional probability distribution of the remaining part of the curve, given γ1, is the same as the unconditional distribution of a whole curve, starting at the tip and ending at r2 in the domain  .
.

 (8K)
(8K)
Fig. 2. The exploration process for the Ising model. At each step the walk turns L or R according to the value of the spin in front of it. The relative probabilities are determined by the expectation value of this spin given the fixed spins either side of the walk up to this time. The walk never crosses itself and never gets trapped.

In the Ising model, for example, if we already know part of the domain wall, the rest of it can be considered as a complete domain wall in a new region in which the left and right sides of the existing part form part of the boundary. This means the path is a history-dependent random walk. It can be seen (Fig. 2) that when the growing tip τ approaches an earlier section of the path, it must always turn away from it: the tip never gets trapped. There is always at least one path on the lattice from the tip τ to the final point r2.
2.2. O (n) model
The loop gas picture of the Ising and percolation models may simply be generalised by counting each closed loop with a fugacity n

| (4) |
This is called the O (n) model, for the reason that it gives the partition function for n-component spins s (r) = (s1 (r), … , sn (r)) with

| (5) |
where Tr sa (r) sb (r) = δab. Following the same procedure as before we obtain the same set of closed loops (and open paths) except that, on summing over the last spin in each closed loop, we get a factor n. The model is called O (n) because of its symmetry under rotations of the spins. The version (5) makes sense only when n is a positive integer (and note that the form of the partition function is different from that of the conventional O (n) model, where the second term is exponentiated). The form in (4) is valid for general values of n, and it gives a probability measure on the loop gas for real n 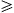 0. However, the dual picture is useful only for n = 1 and n = 2 (see below). As for the case n = 1, there is a critical value xc (n) at which the mean loop length diverges. Beyond this, there is a dense phase.
0. However, the dual picture is useful only for n = 1 and n = 2 (see below). As for the case n = 1, there is a critical value xc (n) at which the mean loop length diverges. Beyond this, there is a dense phase.
Apart from n = 1, other important physical values of n are:
• n = 2. In this case we can view each loop as being oriented in either a clockwise or anti-clockwise sense, giving it an overall weight 2. Each loop configuration then corresponds to a configuration of integer valued height variables h (R) on the dual lattice, with the convention that the nearest neighbour difference h (R′) − h (R) takes the values 0, +1 or −1 according to whether the edge crossed by RR′ is unoccupied, occupied by an edge oriented at 90° to RR′, or at −90°. (That is, the current running around each loop is the lattice curl of h.) The variables h (R) may be pictured as the local height of a crystal surface. In the low-temperature phase (small x) the surface is smooth: fluctuations of the height differences decay exponentially with separation. In the high-temperature phase it is rough: they grow logarithmically. In between is a roughening transition. It is believed that relaxing the above restriction on the height difference h (R′) − h (R) does not change the universality class, as long as large values of this difference are suppressed, for example using the weighting exp [−β (h (R′) − h (R))2]. This is the discrete Gaussian model. It is dual to a model of two-component spins with O (2) symmetry called the XY model.
• n = 0. In this case, closed loops are completely suppressed, and we have a single non-self-intersecting path connecting r1 and r2, weighted by its length. Thus, all paths of the same length are counted with equal weight. This is the self-avoiding walk problem, which is supposed to describe the behaviour of long flexible polymer chains. As x→xc-, the mean length diverges. The region x > xc is the dense phase, corresponding to a long polymer whose length is of the order of the area of the box, so that it has finite density.
• n = −2 corresponds to the loop-erased random walk. This is an ordinary random walk in which every loop, once it is formed, is erased. Taking n = −2 in the O (n) model of non-intersecting loops has this effect.
| <== previous lecture | | | next lecture ==> |
| The Ising and percolation models | | | Potts model |