Potts model

Date: 2015-10-07; view: 402.

Another important model which may described in terms of random curves in the Q-state Potts model. This is most easily considered on square lattice, at each site of which is a variable s (r) which can take Q (initially a positive integer) different values. The partition function is

(6)

with e^βJ = (1 − p)⁻¹. The product may be expanded in a similar way to the case of the Ising model. All possible graphs will appear. Within each connected component of the Potts spins must be equal, giving rise to a factor Q when the trace is performed. The result is

(7)

where is the number of edges in , is the number in its complement, and is the number of connected components of , which are called Fortuin–Kasteleyn (FK) clusters. This is the random cluster representation of the Potts model. When p is small, the mean cluster size is small. As p → p_c, it diverges, and for p > p_c there is an infinite cluster which contains a finite fraction of all the sites in the lattice. It should be noted that these FK clusters are not the same as the spin clusters within which the original Potts spins all take the same value.

The limit Q → 1 gives another realisation of percolation—this time bond percolation on the square lattice. For Q → 0 there is only one cluster. If at the same time x → 0 suitably, all loops are suppressed and the only graphs which contribute are spanning trees, which contain every site of the lattice. In the Potts partition function each possible spanning tree is counted with the same weight, corresponding to the problem of uniform spanning trees (UST). The ensemble of paths on USTs connecting two points r₁ and r₂ turns out to be be that of loop-erased random walks.

The random cluster model may be realised as a gas of dense loops in the way illustrated in Fig. 3. These loops lie on the medial lattice, which is also square but has twice the number of sites. It may be shown that, at p_c, the weights for the clusters are equivalent to counting each loop with a fugacity . Thus, the boundaries of the critical FK clusters in the Q-state Potts model are the same in the scaling limit (if it exists) as the closed loops of the dense phase of the O (n) model, with .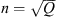

(8K)

Fig. 3. Example of FK clusters (heavy lines) in the random cluster representation of the Potts model, and the corresponding set of dense loops (medium heavy) on the medial lattice. The loops never cross the edges connecting sites in the same cluster.

To generate an open path in the random cluster model connecting sites r₁ and r₂ on the boundary we must choose ‘wired' boundary conditions, in which p = 1 on all the edges parallel to the boundary, from r₁ to r₂, and free boundary conditions, with p = 0, along the remainder.