Restriction

Date: 2015-10-07; view: 382.

It is also interesting to work out how the local scale transforms in going from a_t to ã_t. A measure of this is . A similar calculation starting from (22) gives, in the same limit as above

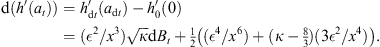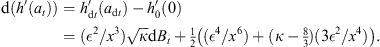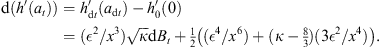
(24)

Now something special happens when κ = 8/3. The drift term in d (h′ (a_t)) does not then vanish, but if we take the appropriate power it does. This implies that the mean of is conserved. Now at t = 0 it takes the value , where Φ_A = h₀ is the map that removes A. If K_t hits A at time T it can be seen from (22) that . On the other hand, if it never hits A then 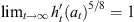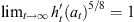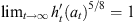. Therefore, gives the probability that the curve γ does not intersect A.

This is a remarkable result in that it depends only on the value of at the starting point of the SLE (assuming of course that Φ_A is correctly normalised at infinity). However, it has the following even more interesting consequence. Let . Consider the ensemble of all SLE_8/3 in H, and the sub-ensemble consisting of all those curves γ which do not hit A. Then the measure on the image in H is again given by SLE_8/3. The way to show this is to realise that the measure on γ is characterised by the probability P (γ ∩ A′ = ) that γ does not hit A′ for all possible A′. The probability that does not hit A′, given that γ does not hit A, is the ratio of the probabilities 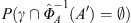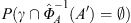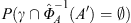and P (γ ∩ A = ). By the above result, the first factor is the derivative at the origin of the map which removes A then A′, while the second is the derivative of the map which removes A. Thus

(25)

Since this is true for all A′, it follows that the law of given that γ does not intersect A is the same as that of γ. This is called the restriction property. Note that while, according to Property 3.2, the law of an SLE in any simply connected subset of H is determined by the conformal mapping of this subset to H, the restriction property is stronger than this, and it holds only when κ = 8/3.

We expect such a property to hold for the continuum limit of self-avoiding walks, assuming it exists. On the lattice, every walk of the same length is counted with the same weight. That is, the measure is uniform. If we consider the sub-ensemble of such walks which avoid a region A, the measure on the remainder should still be uniform. This will be true if the restriction property holds. This supports the identification of self-avoiding walks with SLE_8/3.