
Radial SLE and the winding angle
Date: 2015-10-07; view: 544.
So far we have discussed a version of SLE that gives a conformally invariant measure on curves which connect two distinct boundary points of a simply connected domain  . For this reason it is called chordal SLE. There are variants which describe other situations. For example, one could consider curves γ which connect a given point r1 on the boundary to an interior point r2. The Riemann mapping theorem allows us to map conformally onto another simple connected domain, with r2 being mapped to any preassigned interior point. It is simplest to choose for the standard domain the unit disc U, with r2 being mapped to the origin. So we are considering curves γ which connect a given point eiθ0 on the boundary with the origin. As before, we may consider growing the curve dynamically. Let Kt be the hull of that portion which exists up to time t. Then there exists a conformal mapping gt which takes U
. For this reason it is called chordal SLE. There are variants which describe other situations. For example, one could consider curves γ which connect a given point r1 on the boundary to an interior point r2. The Riemann mapping theorem allows us to map conformally onto another simple connected domain, with r2 being mapped to any preassigned interior point. It is simplest to choose for the standard domain the unit disc U, with r2 being mapped to the origin. So we are considering curves γ which connect a given point eiθ0 on the boundary with the origin. As before, we may consider growing the curve dynamically. Let Kt be the hull of that portion which exists up to time t. Then there exists a conformal mapping gt which takes U  Kt to U, such that gt (0) = 0. There is one more free parameter, which corresponds to a global rotation: we use this to impose the condition that
Kt to U, such that gt (0) = 0. There is one more free parameter, which corresponds to a global rotation: we use this to impose the condition that  is real and positive. One can then show that, as the curve grows, this quantity is monotonically increasing, and we can use this to reparametrise time so that
is real and positive. One can then show that, as the curve grows, this quantity is monotonically increasing, and we can use this to reparametrise time so that  . This normalised mapping then takes the growing tip τt to a point eiθt on the boundary.
. This normalised mapping then takes the growing tip τt to a point eiθt on the boundary.
Loewner's theorem tells us that  , when expressed as a function of gt (z), should be holomorphic in
, when expressed as a function of gt (z), should be holomorphic in  apart from a simple pole at eiθt. Since gt preserves the unit circle outside
apart from a simple pole at eiθt. Since gt preserves the unit circle outside  should be pure imaginary when |gt (z)| = 1, and in order that
should be pure imaginary when |gt (z)| = 1, and in order that  , it should approach 1 as gt (z) → 0. The only possibility is
, it should approach 1 as gt (z) → 0. The only possibility is

| (26) |
This is the radial Loewner equation. In fact this is the version considered by Löewner [4].
It can now be argued, as before, that given lk and lk (suitably reworded to cover the case when r2 is an interior point) together with reflection, θt must be proportional to a standard Brownian motion. This defines radial SLE. It is not immediately obvious how the radial and chordal versions are related. However, it can be shown that, if the trace of radial SLE hits the boundary of the unit disc at eiθt1 at time t1, then the law of Kt in radial SLE, for t < t1, is the same chordal SLE conditioned to begin at eiθ(0) and end at eiθt1, up to a reparametrisation of time. This assures us that, in using the chordal and radial versions with the same κ, we are describing the same physical problem.
However, one feature that the trace of radial SLE possesses which chordal SLE does not is the property that it can wind around the origin. The winding angle at time t is simply θt − θ0. Therefore, it is normally distributed with variance κt. At this point we can make a connection to the Coulomb gas analysis of the O (n) model in Section 2.4.1, where it was shown that the variance in the winding angle on a cylinder of length L is asymptotically (4/g)L. A semi-infinite cylinder, parametrised by w, is conformally equivalent to the unit disc by the mapping z = e−w. Asymptotically, Re w → Re w − t under Loewner evolution. Thus, we can identify L 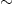 t and hence
t and hence
| κ=4/g. | (27) |
| <== previous lecture | | | next lecture ==> |
| Restriction | | | Identification with lattice models |