
The fractal dimension of SLE
Date: 2015-10-07; view: 541.
Critical exponents from SLE
Many of the critical exponents which have previously been conjectured by Coulomb gas or CFT methods may be derived rigorously using SLE, once the underlying postulates are assumed or proved. However SLE describes the measure on just a single curve, and in the papers of LSW a great deal of ingenuity has gone into showing how to relate this to all the other exponents. There is not space in this article to do these justice. Instead we describe three examples which give the flavour of the arguments, which initially may appear quite unconventional compared with the more traditional approaches.
The fractal dimension of any geometrical object embedded in the plane can be defined roughly as follows: let N (  ) be the minimum number of small discs of radius
) be the minimum number of small discs of radius  required to cover the object. Then if N(
required to cover the object. Then if N(  )
) 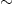
 -df as
-df as  → 0, df is the fractal dimension.
→ 0, df is the fractal dimension.
One way of computing df for a random curve γ in the plane is to ask for the probability P (x, y,  ) that a given point ζ = x + iy lies within a distance
) that a given point ζ = x + iy lies within a distance  of γ. A simple scaling argument shows that if P behaves like
of γ. A simple scaling argument shows that if P behaves like  δf (x, y) as
δf (x, y) as  → 0, then δ = 2 − df. We can derive a differential equation for P along the lines of the previous calculation. The only difference is that under the conformal mapping
→ 0, then δ = 2 − df. We can derive a differential equation for P along the lines of the previous calculation. The only difference is that under the conformal mapping  . The differential equation (written for convenience in cartesian coordinates) is
. The differential equation (written for convenience in cartesian coordinates) is

| (34) |
Now P is dimensionless and therefore should have the form (  /r)2-df times a function of the polar angle θ. In fact, the simple ansatz P=
/r)2-df times a function of the polar angle θ. In fact, the simple ansatz P=  2-dfyα(x2+y2)β, with α + 2β = df − 2 satisfies the equation. [The reason this works is connected with the simple form for the correlator
2-dfyα(x2+y2)β, with α + 2β = df − 2 satisfies the equation. [The reason this works is connected with the simple form for the correlator  Φ2
Φ2  2,1
2,1  2,1
2,1  discussed in Section 5.4.1.] This gives α = (κ − 8)2/8κ, β = (κ − 8)/2κ, and
discussed in Section 5.4.1.] This gives α = (κ − 8)2/8κ, β = (κ − 8)/2κ, and
| df=1+κ/8. | (35) |
This is correct for κ  8: otherwise there is another solution with α = β = 0 and df = 2. A more careful statement and proof of this result can be found in [31].
8: otherwise there is another solution with α = β = 0 and df = 2. A more careful statement and proof of this result can be found in [31].
We see that the fractal dimension increases steadily from the value 1 when κ = 0 (corresponding to a straight line) to a maximum value of 2 when κ = 8. Beyond this value γ becomes space-filling: every point in the upper half plane lies on the curve.
| <== previous lecture | | | next lecture ==> |
| Crossing probability | | | Crossing exponent |