Линейная независимость вектора. Базис. Прямоугольная система координат.

Date: 2015-10-07; view: 422.

13.

линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, то есть коэффициенты единственной такой линейной комбинации равны нулю, множество называется линейно независимым.

Система К из векторов называется линейно зависимой, если существуют такие числа , не все равные нулю одновременно, что

Система К из векторов называется линейно независимой, если равенство возможно только при , т.е. когда линейная комбинация в левой части равенства тривиальная.

Один вектор 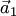тоже образует систему: при — линейно зависимую, а при — линейно независимую.

Свойства линейно зависимых и линейно независимых векторов.

1. Если в систему векторов входит нулевой вектор, то она линейно зависима.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.

4. Система из векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов линейно независима, а после присоединения к ней вектора оказывается линейно зависимой, то вектор можно разложить по векторам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

базис в векторном пространстве — это упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства разложим по ней.

Некоторые свойства базиса :

Единственная тривиальная линейная комбинация векторов базиса возможна только при тривиальном наборе коэффициентов.

Для любого вектора существует единственное представление в виде линейной комбинации соответствующего базиса.

Количество векторов базиса не зависит от выбора базисных векторов и называется размерностью пространства (обозначается dimV).

Представление вектора в виде линейной комбинации базисных векторов называется разложением вектора по данному базису.

Прямоугольная система координат.

Горизонтальная прямая X`X носит название — Ось абсцисс.

Вертикальная прямая Y`Y носит название — Ось ординат.

Точка их пересечения O, носит название — Начало координат или просто начало.

Положение точки на плоскости определяется двумя координатами. Простейший способ таков.

Проводятся две взаимно перпендикулярные прямые X'X, Y'Y. Они называются осями координат. Одна из них X'X (обычно ее проводят горизонтально называется осью абсцисс, другая Y'Y - осью ординат. Точка O их пересечения называется началом координат. Для измерения отрезков на осях координат выбирается некоторая единица масштаба.

На каждой оси выбирается положительное направление (обозначаемое стрелкой). Принято выбирать положительные направления так, чтобы положительный луч OX после поворота на 90° против часовой стрелки совмещался с положительным лучом OY.

Оси координат X'X, Y'Y (с установленными положительными направлениями и выбранным масштабом) образуют прямоугольную систему координат.