
Окружность
Date: 2015-10-07; view: 440.
Эллипс. Определение. Вывод канонического уравнения.
Эллипсом называется геометрическое место всех точек плоскости, сумма расстояний от которых до фокусов есть величина постоянная, большая, чем расстояние между фокусами. 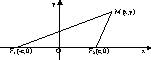
Т.к. MF1 + MF2 = 2a

Т.к. 
То получаем 
Или  .
.
Уравнение 
определяет окружность радиуса R с центром C(а=0; в=0).
Если центр окружности совпадает с началом координат, то есть если , , то уравнение (1) принимает вид: 
23 Парабола. Определение.
Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0. 
Пусть M(x;y) – произвольная точка M с F. Проведем отрезок MN перпендикулярно директрисе. Согласно
определению MF=MN.


24. Гипербола. Определение.
Гиперболой называется множество всех точек плоскости, модуль разности
расстояний от каждой из которых до фокусов есть величина постоянная.
Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению
гиперболы |MF1 – MF2|=2a или MF1 – MF2
=±2a,

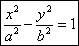

| <== previous lecture | | | next lecture ==> |
| Взаимное расположение прямых и плоскостей. | | | Сложение. |