
The Mode
Date: 2015-10-07; view: 462.
The value that occurs most often in a data set is called the mode.
Example:
The following data give the GPA of 7 students
3.6; 3.2; 2.8; 3.6; 3.8; 3.6; 2.9
Find the mode.
Solution:
It is helpful to arrange the data in order, although it is not necessary
2.8; 2.9; 3.2; 3.6; 3.6; 3.6; 3.8
Since 3.6 occurs three times and 3.6 has a frequency larger than any
other number- the mode for the data set is 3.6.
A data set can have more than one mode or no mode at all, whereas it
will have only one mean and only one median.
A data set with each value occurring only once has no mode.
A data set with two (or more) values occurring with the same (highest)
frequency has two (or more) modes.
Example:
Find the mode of the set data set:
2, 3, 3, 1, 2, 7, 7, 3, 1, 2
Solution:Since 2 and 3 both occur three times, the modes are 2 and 3.
This data set is said to be bimodal.
Example:
Last year's income of six randomly selected families were
210.000, 300.000, 325.000, 280.000, 315.000, 410.000
Find the mode.
Solution:
Since each value occurs only once, there is no mode.
Remark: One advantage of the mode is that it can be calculated for
both kinds of data, quantitive and qualitaive, whereas the mean and
median can be calculated only for quantitive data.
Example:
6 students are selected at random. Their statuses are:
Senior, sophomore, senior, junior, senior, sophomore.
Find the mode.
Solution:
Since senior occurs more frequently than the other categories, it is the
mode for this data set. However, we can not calculate the mean and
median for this data set.
For a data set, the mean, median, and mode can be quite different.
Consider the following example.
Example:
The number of days the first six heart transplant patients survived after their operations were
15; 3; 46; 623; 126; 64
Find the mean, median, and mode.
Solution:
The sample mean is
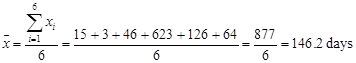
To find median, first we rank the data. The ordered values are
3, 15, 46, 64, 126, 623 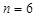
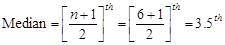
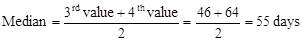 .
.
Since each value occurs only once, there is no mode.
In this example, the mean is much higher than the median. Only 1 out of 6 patients survived longer than 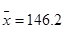 days. It is because of only large survival time that greatly inflates the mean. In this and similar situations, the median should be used as the measure of central tendency.
days. It is because of only large survival time that greatly inflates the mean. In this and similar situations, the median should be used as the measure of central tendency.
To sum up, we can not conclude which of the three measures of central tendency is a better measure overall. Each of them may be better under different situations. But the mean is the most used measure of central tendency. The advantage of the mean is that its calculation includes each value of the data set.
| <== previous lecture | | | next lecture ==> |
| The median | | | Exercises |