
Measures of dispersion for ungrouped data
Date: 2015-10-07; view: 490.
Answers
1. a) 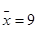 ;
;  ; b)
; b) 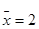 ;
; 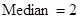 ; 2.
; 2. 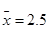 ;
;
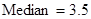 ;
; 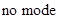 ; 3. a) 8; b) 7, 8; 4.
; 3. a) 8; b) 7, 8; 4. 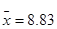 ;
;  ;
;
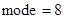 ; 5.
; 5. 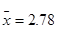 ;
; 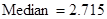 ;
; 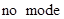 ;6.
;6. 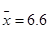 ;
;
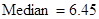 ;
;  ;7.
;7. 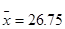 ;
; 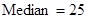 ;
;
8. a) 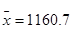 ;
; 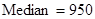 .
.
In statistics, in order to describe the data set accurately statisticians must know more than measures of central tendency. Two data sets with the same mean may have completely different spreads. The variation among values of observations for one data set may be much larger or smaller than for the other data set.
Remark:
The words dispersion, spread, and variation have the same meaning.
Example:
Consider the following two samples:
Sample1: 66, 66, 66, 67, 67, 67, 68, 69
Sample2: 43, 44, 50, 54, 67, 90, 91, 97
The mean of sample1 is 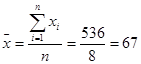
The mean of sample2 is 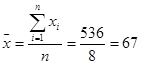 .
.
Each of these samples has a mean equal to 67. However, the dispersion of the observations in the two samples differs greatly. In the first sample all observations are grouped within 2 units of the mean. Only one observation (67) is closer than 13 units to the mean of the second sample, and some are as far away as 30 units. Thus, the mean, median, or mode is usually not by itself a sufficient measure to reveal the shape of the distribution of a data set. We also need a measure that can provide some information about the variation among data values. The measures that help us to know about the spread of data set are called the measures of dispersion. The measures of central tendency and dispersion taken together give a better picture of a data set than measure of central tendency alone. Several quantities that are used as measures of dispersion are the range, the mean absolute deviation, the variance, and the standard deviation.
| <== previous lecture | | | next lecture ==> |
| Exercises | | | The mean absolute deviation |