The mean absolute deviation

Date: 2015-10-07; view: 345.

Range

The simplest measure of variability for a set of data is the range.

Definition:

The range for a set of data is the difference between the largest and smallest values in the set.

Range=Largest value-Smallest value

Example:

Find the range for the sample observations

13, 23, 11, 17, 25, 18, 14, 24

Solution:

We see that the largest observation is 25 and the smallest observation

is 11. The range is 25-11=14.

Example:

A sample is composed of the observations

67, 79, 87, 97, 93, 57, 44, 80, 47, 78, 81, 90, 88, 91

Find the range.

Solution:

The largest observation is 97; the smallest observation is 44.

The range is .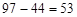

The mean absolute deviation is defined exactly as the words indicate. The word “deviation” refers to the deviation of each member from the mean of the population. The term “absolute deviation” means the numerical (i.e. positive) value of the deviation, and the “mean absolute deviation” is simply the arithmetic mean of the absolute deviations.

Let 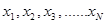denote the 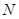members of a population, whose mean is 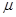. Their mean absolute deviation, denoted by 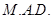is

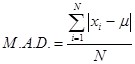
For the sample of 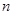observations, with mean 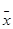, mean absolute deviation is defined analogously

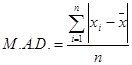
To calculate mean absolute deviation it is necessary to take following steps:

1. Find 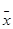(or )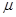

2. Find and record the signed differences

3. Find and record the absolute differences

4. Find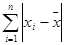

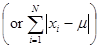
5. Find the mean absolute deviation.

Example:

Suppose that sample consists of the observations

21, 17, 13, 25, 9, 19, 6, and 10

Find the mean absolute deviation.

Solution:

Perhaps the best manner to display the computations in steps 1, 2, 3, and 4 is to make use of a table 1.1 composed of three columns Table 1.1

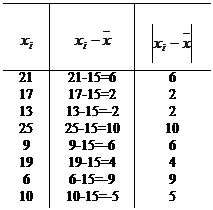
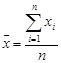
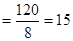
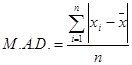
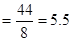
120 44

On the average, each observation is 5.5 units from the sample.