
Характеристическим многочленом матрицы
Date: 2015-10-07; view: 539.
Характеристический многочлен матрицы. Собственные векторы и собственные значения матрицы, их свойства. Запись квадратичной формы в матричном виде.
A= 
называется равный нулю определитель
 ,
,
где  - это переменная. После раскрытия определителя получим многочлен, корни которого называются собственными числами.
- это переменная. После раскрытия определителя получим многочлен, корни которого называются собственными числами.
Пусть  - собственное число матрицы А. Собственным вектором
- собственное число матрицы А. Собственным вектором  матрицы А называется вектор, удовлетворяющий условию
матрицы А называется вектор, удовлетворяющий условию  . Собственные вектора, соответствующие различным собственным числам, ортогональны. Собственный вектор
. Собственные вектора, соответствующие различным собственным числам, ортогональны. Собственный вектор  является решением системы линейных уравнений.
является решением системы линейных уравнений.

Определение 8.1.Матрица  размерности N,называется симметричной (относительно главной диагонали), если
размерности N,называется симметричной (относительно главной диагонали), если  (
(  ).
).
Теорема 8.1. Все собственные числа симметричной матрицы- это действительные числа.
Пример 13.Найти собственные числа и собственные векторы матрицы  .
.
Решение. Составляем характеристическое уравнение

или
 откуда
откуда 
 ,
,  .
.
Находим собственный вектор, соответствующий характеристическому числу  . Из системы уравнений
. Из системы уравнений

(одно из уравнений этой системы есть следствие двух других и может быть отброшено), получим  ,
,  . Полагаем
. Полагаем  , тогда
, тогда  ,
,  и
и  .
.
Находим собственный вектор, соответствующий значению  . Получаем систему уравнений
. Получаем систему уравнений

Одно из этих уравнений может быть отброшено. Отсюда  и
и  .
.
Находим собственный вектор, соответствующий значению  . Получаем систему уравнений
. Получаем систему уравнений

Одно из этих уравнений может быть отброшено. Отсюда  ,
,  ,
,  и
и  .
.
Итак, собственные векторы заданной матрицы имеют вид  ,
,  ,
,  .
.
8.1 Найдите собственные числа и собственные вектора матриц. Собственные вектора будут включать неопределённые константы. Проверьте выполнение условия  . Из системы собственных векторов выделите ортонормированную систему векторов.
. Из системы собственных векторов выделите ортонормированную систему векторов.
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
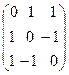
11.  12.
12. 
Квадратичной формой действительных переменных  называется многочлен второй степени относительно этих переменных, не содержащих свободного члена и членов первой степени.
называется многочлен второй степени относительно этих переменных, не содержащих свободного члена и членов первой степени.
Если  - квадратичная форма переменных
- квадратичная форма переменных  , а
, а  — какое– нибудь действительное число, то
— какое– нибудь действительное число, то  .
.
Если n=2, то
 .
.
Если n=3, то
 .
.
Матрица

называется матрицей квадратичной формы.
Пусть  — это собственные числа матрицы А, тогда ортонормированная система собственных векторов матрицы A
— это собственные числа матрицы А, тогда ортонормированная система собственных векторов матрицы A
 ,
,  ,
, 
задаёт ортогональное преобразование координат

которое приводит квадратичную форму  к нормальному виду
к нормальному виду  .
.
8.2 Приведите квадратичную форму ортогональным преобразованием к нормальному виду.
1.  2.
2.  3.
3.  4.
4. 
5.  6.
6. 
| <== previous lecture | | | next lecture ==> |
| Ранг системы векторов. Теорема о ранге матрицы. | | | Список обозначений. |