Ранг системы векторов. Теорема о ранге матрицы.

Date: 2015-10-07; view: 462.

Теорема 7.1.Ниже перечислены преобразования, не изменяющие ранг матрицы.

· Любые две строки можно менять местами.

· Любую строку можно разделить (или умножить) на некоторое не нулевое число.

· Строку i можно прибавить к другой строке j (отнять из строки j) и результат записать вместо строки j. При этом складываются (вычитаются) элементы, стоящие в одном и том же столбце.

· Любую строку можно разделить (или умножить) на некоторое не нулевое число, получившуюся строку отнять из некоторой другой строки j и результат записать вместо строки j.

· Транспонирование.

· Любые два столбца можно менять местами.

· Любой столбец можно разделить (или умножить) на некоторое не нулевое число.

· Столбец i можно прибавить к другому столбцу j (отнять из столбца j) и результат записать вместо столбца j. При этом складываются (вычитаются) элементы, стоящие в одной и той же строке.

· Любой столбец можно разделить (или умножить) на некоторое не нулевое число, получившийся столбец отнять из некоторого другого столбца j и результат записать вместо столбца j.

Теорема 7.2Ранг матрицы после приведения её при помощи элементарных преобразований к верхнетреугольному виду равен числу ступенек .

Пример 9. Найти ранг матрицы .

Решение. Пользуясь элементарными преобразованиями, не изменяющими ранг матрицы, упростим матрицу.

1. Переставим первый и второй столбец матрицы. Умножим первую строку на 0.5.

2. Прибавим к третьему столбцу удвоенный первый столбец. Прибавим некоторое кратное первой строки к каждой из остальных строк.

3. Умножим вторую строку на –1. Вычтем из третьего столбца удвоенный второй столбец. Вычитая из третьей и пятой строк некоторые кратные новой второй строки, приходим к искомой диагональной форме.

Ранг исходной матрицы равен двум.

Рассмотрим матрицу А, произвольной размерности ( ). Минором порядка К для данной матрицы А будем называть определитель порядка К с элементами, лежащими на пересечении любых К строк и любых К столбцов, где , .

Например:

.

Матрица A ( ) имеет двенадцать миноров 1-го порядка, они совпадают с элементами матрицы; 18 миноров 2-го порядка и 4 минора третьего порядка.

Предположим, что хотя бы один из элементов матрицы А отличен от нуля, тогда найдём целое положительное число r, для которого будут выполнены условия: 1) у матрицы А имеется минор порядка r, отличный от нуля, 2) всякий минор порядка (r+1) и выше либо равен нулю, либо не существует. Число r, удовлетворяющее требованиям 1) и 2), называется рангом матрицы А.

Из сказанного вытекает ещё одно определение ранга: рангом матрицы А называется число r, равное наивысшему порядку минора, отличного от нуля. Всякий отличный от нуля минор, ранг (т. е. порядок) которого равен рангу этой матрицы, называется базисным минором.

Следует отметить, что ранг матрицы не будет изменяться, если над строками, столбцами матрицы производить элементарные преобразования, а именно:

1) Умножать строки (столбцы) на не нулевые числа.

2) Переставлять местами две строки или два столбца.

3) К какой-либо строке (столбцу) прибавлять другие строки (столбцы), умноженные на ненулевые числа.

4) Строку (столбец), состоящую из одних нулей можно удалить из матрицы.

Ранг матрицы А будем обозначать r(A). Если , то матрицы А и В будут эквивалентны. В этом случае пишут .

Пример 10. Определить ранг матрицы

Решение.Все миноры второго и третьего порядков данной матрицы равны нулю, миноры же первого порядка (сами элементы матрицы) отличны от нуля, поэтому ранг матрицы равен 1.

Пример 11. Определить ранг матрицы

Решение. Рассмотрим определитель минора

Все миноры более высокого порядка, содержащие матрицу

, имеют равный нулю определитель, т.е.

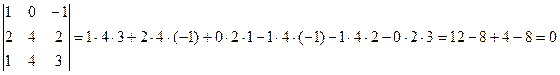и

,

поэтому ранг матрицы А равен 0.

Пример 12. Определить ранг матрицы

Решение. Элементарными преобразованиями из данную матрицу А приведём к треугольному виду. Для этого: a) первую строку умножим на 2 и вычтем из второй, первую строку умножим на 3 и вычтем из третьей; б) вторую строку вычтем из третьей. Получим:

~ ~

Ранг матрицы

равен 3, поскольку её определитель не равен нулю, поэтому ранг исходной матрицы А равен 3.

6.1 Вычислите ранг матриц из упражнения 2.1. Проверьте утверждение о том, что если ранг квадратной матрицы меньше её размерности, то определитель такой матрицы равен нулю.