
Векторная алгебра.
Date: 2015-10-07; view: 798.
Векторы представляют собой направленные отрезки в пространстве, имеющие определенную длину. Вектор - отрезок определенной длины, одна из ограничивающих точек которого принята за начало, а другая – за конец.
Длина вектора (модуль) – расстояние между ограничивающими его точками.
К векторам относится и нуль-вектор, у которого начало и конец совпадают.
Определение:Векторы называются коллинеарными, если они располагаются на одной
прямой или на параллельных прямых, то есть если существует прямая, которой они параллельны.
Определение:Векторы называются компланарными, если они лежат в одной
плоскости или если существует плоскость, которой они параллельны. Если компланарные векторы имеют общее начало, то они лежат в одной плоскости.
Определение: Векторы называются равными, если они имеют равные модули,
коллинеарны и направлены в одну сторону. (Если вектора направлены в противоположные стороны при равных модулях и наличии коллинеарности, то они противоположны).
Вектор можно переносить параллельно самому себе, помещая его начало в любую
точку пространства.
Сложение векторов
Пусть даны два вектора а и b.
1. Возьмем произвольную точку 0 и построим вектор ОА=a, потом от этой же точки отложим вектор ОВ=b. Построим на этих векторах, как на сторонах, параллелограмм OAСB. Вектор ОС, являющийся диагональю параллелограмма, проведенной из вершины 0, и будет суммой векторов а+b.
А С
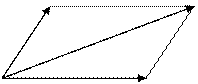
a a+b
О b В
2. От произвольной точки 0 отложим вектор ОА=а , затем от точки А отложим вектор АВ=b. Вектор, соединяющий начало первого слагаемого с концом второго, будет суммой этих векторов ОВ=а+b.



 А
А
| <== previous lecture | | | next lecture ==> |
| Векторное пространство. | | | A b a b |