Системы координат

Date: 2015-10-07; view: 713.

O b B

Если на векторах a и b, отложенных из общей точки, построить параллелограмм, то вектор OC (одна диагональ параллелограмма) равен сумме a+b, а вектор BA (другая диагональ) равен разности a-b.

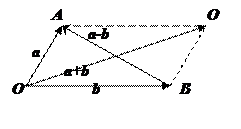Умножение вектора на скаляр.

Пусть даны вектор a и число λ. Произведением вектора a на число λ называется вектор с, коллинеарный вектору а, имеющий длину |с|=|λ|×|а| и то же направление, что и вектор а, если λ>0, и противоположное направление, если λ<0.

Из определения умножения вектора на число следует, что если b=λa, то векторы b и a коллинеарны. Очевидно, что из коллинеарности векторов следует, что b=λa.

Определение:вектора a и b коллинеарны тогда и только тогда, когда имеет

место равенство b=λa.

1). Для любых чисел λ и γ и любого вектора а справедливо равенство λ(γа)=(λγ)а.

2). Пусть существует вектор а не равный нулю. Для любого коллинеарного ему вектора b существует, и притом только одно λ, удовлетворяющее равенству: b=λa.

Это число либо λ=|b|/|a|, либо λ=-|b|/|a| в зависимости от того направлены ли вектора a и bодинаково или противоположно.

Умножение вектора на число обладает распределительным свойством λ(a+b)=λa+λb, (λ₁+λ₂)a=λ₁a+λ₂a.

Вектор, длина которого равна единице, называется единичным.

Каждый вектор равен произведению его модуля на единичный вектор того же направления (это следует из определения умножения вектора на число).

Угол между двумя векторами.

Пусть даны два произвольных вектора a и b. Отложим от произвольной точки векторы OA=a, OB=b. Угол между векторами – это угол, на который надо повернуть один из векторов до его совпадения со вторым.

Рассмотрим ось l, положительное направление которой совпадает с направлением единичного вектора l^°, расположенного на оси. Тогда, углом между вектором и осью будет угол между векторами а, l^°.

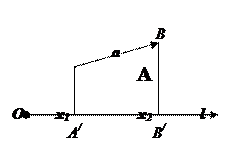Проекция вектора на ось и составляющая вектора по оси.

 

Проекцией вектора a на ось l называется длина отрезка A^/B^/, заключенного между основаниями перпендикуляров, опущенных на ось из начала и конца вектора a, которой приписан знак «+», если отрезок A^/B^/ ориентирован в положительную сторону относительно 0l и знак “-“, если наоборот.

 

 

 

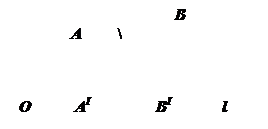
Теорема 1:Проекция вектора а на ось l равна модулю вектора а, умноженному на косинус угла между вектором и осью: ПР_Ol(a)=|a|cosφ.

Теорема 2: проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось AC=AB+BC; ПР_OlAC=ПР_Ol(AB)+ПР_Ol(BC)

Теорема 3: если вектор a умножить на число λ, то его проекция на ось также умножится на это число: ПР_Ol(λa)=λ×ПР_Ol(a)

Определение: вектор, соединяющий проекцию начала вектора а с проекцией его конца, называется составляющей вектора а по оси Ol: сост.Ol=ПР_Ola×l^°=AB.

Линейная зависимость векторов.

Векторы a₁,a₂,…,a_k называются линейно зависимыми, если существуют числа λ₁, λ₂,…,λ_к, не все равные нулю, для которых имеет место равенство λ₁а₁+λ₂а₂+…+λ_ка_к=0.

Векторы а₁,а₂,…,а_к называются линейно независимыми, если равенство (I) имеет место только при λ₁=λ₂=…=λ_к=0 (то есть в тривиальном случае).

Полагая, что, например, λ₁≠0 запишем: а₁=-(λ₂а₂)/λ₁-(λ₃а₃)/λ₁-…-(λ_ка_к)/λ₁

Выражение в правой части – линейная комбинация векторов а₂,а₃,…,а_к.

Если несколько векторов линейно зависимы, то хотя бы один из них всегда можно представить в виде линейной комбинации остальных (верно и обратное).

Линейная зависимость векторов на плоскости.

Теорема 1:всякие три вектора a, b, c на плоскости линейно зависимы.

Доказательство: нужно доказать, что один из векторов является линейной комбинацией остальных.

1) среди векторов есть пара коллинеарных, пусть a и b, то есть a=λb или a=λb+0×c, то есть a есть линейная комбинация b и c.

2) Коллинеарных векторов нет.

Перенесем все три вектора в общее начало.

 

 

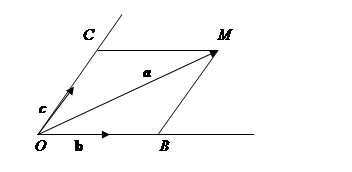Через конец вектора a проведем прямые, параллельные векторам c и b до пересечения с прямыми, на которых находятся вектора b и c. Тогда, очевидно, что OM=OC+OB, но OC и OB коллинеарны b и c соответственно, то есть OC=λ₁c; OB=λ₂b.

Поэтому, a=λ₁c+λ₂b, то есть является линейной комбинацией векторов b и c.

Следствие:Если число данных векторов на плоскости больше трех, то они также линейно зависимы, то есть один из них можно представить в виде линейной комбинации остальных.

Доказательство: пусть даны а₁,а₂,…,а_к; к>3

Из теоремы имеем а₁=μ₂а₂+μ₃а₃

Тогда для k векторов а₁=μ₂а₂+μ₃а₃+…+0×а_k, что и требовалось доказать.

Теорема 2:Для того, чтобы два вектора на плоскости были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны.

Два коллинеарных вектора линейно зависимы.

Максимальное число линейно независимых векторов на плоскости равно двум.

 

Линейная зависимость в пространстве.

Теорема 3: всякие четыре вектора a, b, c, d в пространстве линейно зависимы.

 

Доказательство: Пусть все векторы имеют общее начало. Покажем, что один из векторов является линейной комбинацией остальных.

 

1) Пусть среди них есть тройка компланарных (a, b, c). Так как все компланарные векторы выходят из одной точки, то значит, они лежат в одной

плоскости, а по теореме I они линейно зависимы, то есть один можно записать в виде линейной комбинации остальных: а=μ₂b+μ₃c

И для четырех: a=μ₂b+μ₃c+0×d, то есть a – линейная комбинация b, c, d.

2) Среди них нет тройки компланарных.

Тогда вектор а можно представить в виде суммы трех векторов, коллинеарных соответственно b,c,d.

 

 

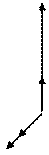
Для этого через точку M проведем плоскости параллельные трем

плоскостям, определяемым парами b,c; c,d; d,b, и получим параллелепипед с диагональю а=OM. Очевидно, а=OM=OM₁+M₁P+PM.

Но OM₁=λ₁b, M₁P=OM₂=λ₂c, PM=OM₃=λ₃d.

Следовательно, a=λ₁b+λ₂c+λ₃d, то есть a,b,c,d линейно зависимы.

Следствие: 1) Если число векторов в пространстве больше четырех, то они линейно зависимы.

3) для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы они были линейно зависимы.

4) Максимальное число линейно независимых векторов в пространстве равно трем.

Базисом на плоскости называются два любых линейно независимых вектора. Пусть е₁ и е₂ образуют базис. Любой вектор а на плоскости можно представить в виде: а=λ₁е₁+λ₂е₂ (так как три вектора на плоскости линейно зависимы), то есть разложить по базису.

Числа λ₁, λ₂ – аффинные координаты вектора а на плоскости а={λ₁; λ₂}.

Теорема 4: разложение вектора а по базису е₁ и е₂ является единственным.

Доказательство: пусть существует разложение одного вектора а по базису е₁,е₂; а=μ₁е₁+μ₂е₂; а=ν₁е₁+ν₂е₂

Вычтем второе уравнение из первого: 0=(μ₁-ν₁)е₁+(μ₂-ν₂)е₂

Но е₁ и е₂ линейно независимы, поэтому μ₁-ν₁=0; μ₂-ν₂=0, то есть μ₁=ν₁; μ₂=ν₂ и разложение по базису единственно. Базис в пространстве – это три любых линейно независимых вектора. Всякие три некомпланарных вектора образуют базис.

Любой вектор а однозначно разлагается по векторам базиса: а=λ₁е₁+λ₂е₂+λ₃е₃; где λ₁, l_2, λ₃ – аффинные координаты вектора в пространстве.

 

Фиксируем в пространстве т.О и рассматриваем произвольную точку М. Радиусом-вектором т. М по отношению к точке О называется вектор ОМ. Если в пространстве кроме точки О выбран некоторый базис, то точке М можно сопоставить упорядоченную тройку чисел – компоненты ее радиус-вектора.

Определение:декартовой системой координат в пространстве называется совокупность точки и базиса.

Точка носит название начала координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат. Первая – ось абсцисс, вторая – ось ординат, третья – ось аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Рассмотрим прямоугольную систему координат в пространстве Oxyz. На каждой из осей выберем единичный вектор, направление которого совпадает с положительным направлением оси: векторы i, j, k, причем |i|=|j|=|k|=1. Эти три взаимно-перпендикулярных вектора называются ортами. Так как эти орты некомпланарны, то они образуют базис,

называемый декартовым ортогональным. Рассмотрим некоторый вектор а в пространстве, переместим его в точку О, то есть построим ОМ=а. Проведя через конец вектора а плоскости, параллельные координатным осям, получим параллелепипед.

а=ОМ₁+М₁Р+РМ, где М₁Р=ОМ₂; МР=ОМ₃

ОМ₁=ПР_ОхОМ×i, ОМ₂=ПР_ОуОМ×j, ОМ₃=ПР_ОzOM×k.

Обозначим проекции вектора а=ОМ на оси Ox, Oy, Oz – a_x, a_y, a_z.

Тогда, разложение вектора по ортогональному базису будет таким: а=a_xi+a_yj+a_zk.

Это разложение вектора на составляющие по координатным осям. Если проекции вектора а на оси координат равны a_x, a_y, a_z, то можно записать: а={a_x, a_y, a_z}. Это прямоугольные декартовы координаты.

Линейные операции над векторами можно заменить арифметическими действиями над их проекциями:

λа=λa_xi+λa_yj+λa_zk

a±b=(a_x±b_x)i+(a_y±b_y)j+(a_z±b_z)k

Направление вектора в пространстве определяется углами α, β, γ, которые вектор составляет с осями координат.

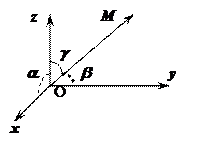Косинусы этих углов называются направляющими косинусами вектора а:

a_x=|a|×cosa, то есть cosa= ;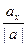

a_y=|a|×cosb, то есть cosb= ;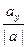

a_z=|a|×cosg, то есть cosg= .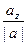

Вектор a=OM – диагональ параллелепипеда, а зная теорему о диагонали прямоугольного параллелепипеда: |OM|²=|OM₁|²+|OM₂|²+|OM₃|² и |a|= 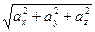; получим cos²a+cos²b+cos²g=1.

Условия коллинеарности двух векторов.

Пусть вектор a=a_xi+a_yj+a_zkи b=b_xi+b_yj+b_zk коллинеарны. Тогда, a=λb. Но при умножении вектора на число его проекции на оси также умножаются на это число. Тогда, a_x=λb_x; a_y=λb_y; a_z=λb_z.

Верно и обратное.

Итак, для коллинеарности двух векторов необходимо и достаточно, чтобы их проекции были пропорциональны: a_x/b_x=a_y/b_y=a_z/b_z.