
Скалярное произведение векторов.
Date: 2015-10-07; view: 708.
Произведение векторов, арифметические векторные пространства, евклидовы пространства.
ЛЕКЦИЯ N5.
Скалярное, векторное, смешанное
1.Скалярное произведение векторов. 19
2. Векторное произведение двух векторов. 20
3. Смешанное (векторно-скалярное) произведение трех векторов. 21
4.Арифметические векторные пространства. 22
Конечномерные евклидовы пространства. 22
5.Ортогональный базис. 23
В практических задачах часто встречаются операции умножения вектора на вектор. Результатом такого умножения может быть либо число, либо вектор. Соответственно рассматривают два вида умножения: скалярное и векторное.
Определение: скалярным произведением векторов а и b называют число, равное произведению модулей перемножаемых векторов на косинус угла φ между ними.
a×b=|a||b|cosφ.
Скалярное произведение двух векторов является числом (скаляром).
Физический смысл: пусть материальная точка двигается по прямой, перемещаясь из положения М в положение N под действием силы F, направление которой образует угол φ с направлением перемещения точки.
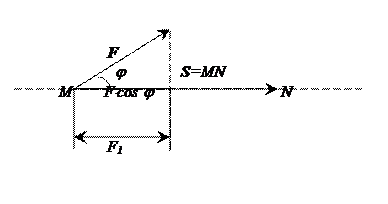 |
Работа постоянной силы на прямолинейном участке пути равна скалярному произведению вектора силы на вектор перемещения. Работа А силы F будет равна, как известно из механики, произведению модуля силы F1, совершающей работу, на величину S пути S=MN:
A=|F1|S=|F||s|cosφ=F×S
Свойства скалярного произведения.
1. Скалярное произведение двух векторов обращается в нуль, если вектора взаимно перпендикулярны или если один сомножитель (или оба) есть нуль-векторы (то есть a×b=0, если cosφ=0, или если а=0 или b=0 или a=b=0).
2. Скалярный «квадрат» вектора равен квадрату его длины: a×a=a2 (так как при a=b угол φ=0 и соs φ=1).
3. Скалярное произведение не изменяет своего значения при перестановке сомножителей (свойство коммутативности) a×b=b×a (так как |a||b|=|b||a| и cos(-φ)=cos φ).
4. Скалярное произведение равно произведению длины одного из перемножаемых векторов на проекцию другого вектора на направление первого; a×b=|a|прab=|b|прba, то есть прab=|b|cosφ; прba=|a|cosφ
5. Скалярное произведение обладает распределительным свойством (a+b)×c=a×c+b×c. Для доказательства воспользуемся свойством 4: (a+b)×c=|c|прc(a+b)=|c|[прca+прcb]
6. Чтобы умножить скалярное произведение на числовой множитель, достаточно на этот множитель умножить один из перемножаемых векторов: m(a×b)=(ma)×b=a×(mb)
Выражение скалярного произведения
через координаты перемножаемых векторов
Пусть даны векторы: a=axi+ayj+azk; b=bxi+byj+bzk
Тогда, a×b=(axi+ayj+azk)(bxi+byj+bzk)
В силу 5 и 6 можно представить это как произведение многочлена на многочлен: a×b=axbxi2+aybxi×j+azbxi×k+axbyi×j+aybyj2+azbyj×k+axbzi×k+aybzj×k+azbzk2=axbx+ayby+azbz
Все произведения, кроме скалярных квадратов, равны нулю, так как входящие в них векторы ортогональны.
Итак, скалярное произведение равно сумме попарных произведений одноименных проекций векторов, так как i2=1,j2=1, k2=1
Условие перпендикулярности векторов может быть таким: axbx+ayby+azbz=0.
Скалярным произведением двух векторов можно воспользоваться для вычисления угла между ними:
Cos φ=(a×b)/|a||b| или cos φ=(axbx+ayby+azbz)/( 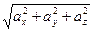
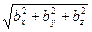 )
)
Отсюда и находим условие перпендикулярности (ортогональности) двух векторов: a×b=0 или axbx+ayby+azbz=0.
| <== previous lecture | | | next lecture ==> |
| Системы координат | | | Векторное произведение двух векторов |