Векторное произведение двух векторов
Date: 2015-10-07; view: 498.
Определение: векторным произведением вектора a на вектор b называется новый вектор с, обозначаемый символом c=a 
b, и определяемый следующими тремя условиями:
1) модуль вектора с равен площади параллелограмма, построенного на векторах a и b (после совмещение их начал), то есть |с|=|a b|=|a||b|sinφ, где φ – угол между векторами a и b.
2) Вектор с перпендикулярен к плоскости этого параллелограмма (то есть перпендикулярен обоим векторам a и b).
3) 
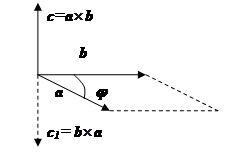Вектор с направлен в ту сторону от этой плоскости, что кратчайший поворот от вектора а к вектору b вокруг вектора с (после совмещения начал всех трех векторов) кажется происходящим против часовой стрелки, если смотреть из конца вектора с (то есть вектора a, b и с должны образовывать правую тройку).
Свойства векторного произведения
1. Векторное произведение двух векторов равно нулю, если один или оба сомножителя являются нуль-векторами (a=0, b=0, или a=b=0), или же, если сомножители являются коллинеарными векторами (φ=0 или φ=π), в частности а а=0.
2. При перестановке местами векторов-сомножителей векторное произведение изменяет знак, то есть превращается в противоположный вектор:
b a=-(a b).
3. Векторное произведение не обладает коммутативностью. В самом деле
с1=-с
4. Векторное произведение векторов обладает распределительным свойством: a (b+c)=(a b)+(a c)
5. Чтобы умножить векторное произведение двух векторов на произвольный числовой множитель, достаточно умножить на него один из перемножаемых векторов (любой): m(a b)=(ma) b=a (mb)
Вычисление векторного произведения
через проекции (координаты)
перемножаемых векторов
a b=(axi+ayj+azk) (bxi+byj+bzk)=axbx(i i)+axby(i j)+axbz(i k)+aybx(j i)+ayby(j j)+aybz(j k)+azbx(k i)+azby(k j)+azbz(k k)=(axby-aybx)k+(azbx-axbz)j+(aybz-azby)i=(aybz-azby)i+(axby-aybx)k+(azbx-axbz)j и это, как нетрудно убедиться, определитель
a b=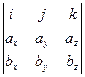 
Замечание: при помощи векторного произведения легко вычислить площадь треугольника, стороны которого заданы векторами или вершины – их координатами.
 |
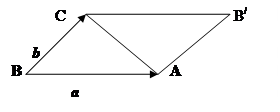Пример: найти площадь треугольника, вершинами которого служат точки А(2, -1, 3),
В(1, 3, -5) и С(0, -2, -3).
Решение: находим векторы a=CA, b=CB; a=(2-0)i+[-1-(-2)]j+[3-(-3)]k=2i+j+6k; b=i+5j-2k
a b=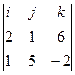 
=-32i+10j+9k
|a b|= 
= 
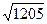
S=1/2× 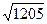≈17,4 (ед2).
| <== previous lecture | | | next lecture ==> |
| Скалярное произведение векторов. | | | Смешанное (векторно-скалярное) произведение трех векторов |