
Линейная алгебра
Date: 2015-10-07; view: 428.
Вариант 30
Вариант 29
Вариант 28
Вариант 27
Вариант 26
Вариант 25
Вариант 24
Вариант 23
Вариант 22
Вариант 21
Вариант 20
Вариант 19
Вариант 18
Вариант 17
Вариант 16
Вариант 15
Вариант 14
Вариант 13
Вариант 12
Вариант 11
Вариант 10
Вариант 9
Вариант 8
Вариант 7
Вариант 6
Вариант 5
Вариант 4
Вариант 3
Вариант 2
Вариант 1
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:  .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:  .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение: 
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?
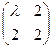
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:

В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:

В6. Найти ранг матрицы методом Гаусса:

В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).

Найдём определитель матрицы системы
detA=  =-3≠0, значит, к системе применим матричный метод. Находим обратную матрицу
=-3≠0, значит, к системе применим матричный метод. Находим обратную матрицу  :
:
 =-
=- 
Запишем решение системы в матричной форме
 =-
=-  ×
×  =-
=-  =
= 
Следовательно,  =2,
=2,  =-5,
=-5,  =3.
=3.
С3. Решить методом Гаусса системы уравнений:
а)  Преобразуем расширенную матрицу системы:
Преобразуем расширенную матрицу системы:


  (чтобы получить на диагонали элемент, отличный от нуля, приходится изменить порядок неизвестных)
(чтобы получить на диагонали элемент, отличный от нуля, приходится изменить порядок неизвестных)


  Полученной матрице
соответствует система
Полученной матрице
соответствует система
 Система неопределенна (r = 3 < n = 5). Неизвестные
Система неопределенна (r = 3 < n = 5). Неизвестные  , ,  , ,  – базисные, – базисные,  , ,  - свободные. Последовательно находим: - свободные. Последовательно находим:
 = -13 = -13  - 2; - 2;  = -2 = -2  -9 -9  +2=
= -2(-13 +2=
= -2(-13  -2) -9 -2) -9  +2=17 +2=17  +6; +6;
 = =  + 2 + 2  +4 +4  - -  +1=
=17 +1=
=17  +6+2(-13 +6+2(-13  -2)+4 -2)+4  - -  +1=
= -5 +1=
= -5  - -  +3
Полагая +3
Полагая  = u, = u,  = ѵ, получаем общее решение системы в виде = ѵ, получаем общее решение системы в виде
 = -u+5ѵ+3, = -u+5ѵ+3,  =u, =u,  =17ѵ+6, =17ѵ+6,  =13ѵ-2, =13ѵ-2,  = ѵ
б) = ѵ
б)
 Преобразуем расширенную матрицу системы:
Преобразуем расширенную матрицу системы:
 
 

 
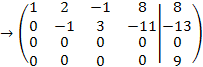 Здесь последовательно выполнили следующие преобразования:
1) Переставили первую и четвертую строки; первую строку, умноженную на 3,2,7, вычли поочередно из второй, третьей, четвертой строк,
2) Вторую строку разделили на 2; вторую строку, умноженную на 1, затем 5, вычли поочередно из третьей, затем четвертой строк.
Последней матрице соответствует система
Здесь последовательно выполнили следующие преобразования:
1) Переставили первую и четвертую строки; первую строку, умноженную на 3,2,7, вычли поочередно из второй, третьей, четвертой строк,
2) Вторую строку разделили на 2; вторую строку, умноженную на 1, затем 5, вычли поочередно из третьей, затем четвертой строк.
Последней матрице соответствует система
 (Уравнение 0=0, соответствующее третьей строке матрицы, отброшено). Мы пришли к системе, содержащей противоречивое уравнение 0=9. Ранги основной матрицы системы и расширенной матрицы не равны. Система несовместима.
(Уравнение 0=0, соответствующее третьей строке матрицы, отброшено). Мы пришли к системе, содержащей противоречивое уравнение 0=9. Ранги основной матрицы системы и расширенной матрицы не равны. Система несовместима.
| |
в)  .
Однородная система всегда имеет решение. Если определитель основной матрицы системы равен нулю, то система имеет множество решений. Если же определитель не равен нулю, то система имеет единственное нулевое решение.
С помощью элементарных преобразований получим: .
Однородная система всегда имеет решение. Если определитель основной матрицы системы равен нулю, то система имеет множество решений. Если же определитель не равен нулю, то система имеет единственное нулевое решение.
С помощью элементарных преобразований получим: 
|
Будем считать базисными переменными  , а свободными
, а свободными  . Имеем систему
. Имеем систему
 Отсюда получим решение:
Отсюда получим решение:

А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 *
*  .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б) 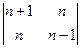 .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в) 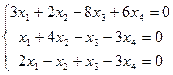 . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:

С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б)  , ,
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
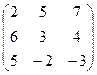 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
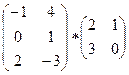 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
| а) | б)  , ,
|
в)  . .
|
А1. Вычислить определитель:
а) 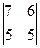 б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
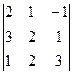 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?
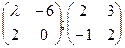
В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а) 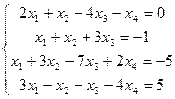 , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
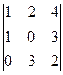 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
Вапвп
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б)  , ,
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
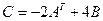 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
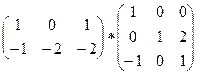 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
б) 
| |
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?
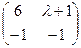
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?
 .
.
А10. Решить матричное уравнение:
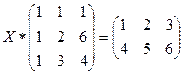 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 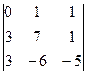
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
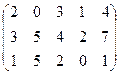 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?
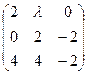
А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 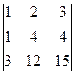
| б) 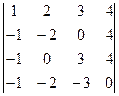
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
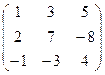 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
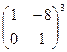 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
А1. Вычислить определитель:
а)  б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить:
 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение:
 .
.
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
 .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

В5. Найти обратную матрицу:
 .
.
В6. Найти ранг матрицы методом Гаусса:
 .
.
В7. Решить методом Гаусса систему уравнений:
 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  , ,
| б) 
|
в)  . .
|
Решение типового варианта
А1. Вычислить определитель:
а)  ; б)
; б) 
 .
.
Определитель второго порядка вычисляется по формуле ( ). Поэтому:
а)  ;
;
б)  .
.
А2. Решить уравнение:
 ,
,
Отсюда следует:  ,
,  .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
По формуле () получим:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).


А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:

Выберем четвертый столбец т.к. в нем содержится больше всего нулей и будем вычислять используя понятие алгебраическое дополнение.

А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
а) Составим главный определитель системы из коэффициентов перед неизвестными 
Составим вспомогательный определитель  из главного путем замены первого столбца на столбец свободных членов
из главного путем замены первого столбца на столбец свободных членов 
Составим вспомогательный определитель  из главного путем замены второго столбца на столбец свободных членов
из главного путем замены второго столбца на столбец свободных членов 
По формулам Крамера получим: 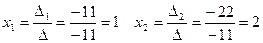
б) Составим главный определитель системы из коэффициентов перед неизвестными  Данный определитель вычисляется любым известным нам способом.
Данный определитель вычисляется любым известным нам способом.
Составим вспомогательный определитель  из главного путем замены первого столбца на столбец свободных членов
из главного путем замены первого столбца на столбец свободных членов 
Составим вспомогательный определитель  из главного путем замены второго столбца на столбец свободных членов
из главного путем замены второго столбца на столбец свободных членов 
Составим вспомогательный определитель  из главного путем замены первого столбца на столбец свободных членов
из главного путем замены первого столбца на столбец свободных членов 
По формулам Крамера получим: 
А7. Найти матрицу  , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 



А8. Вычислить: 
Найдем  , затем найдем
, затем найдем

А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

Т.к матрица имеет себе обратную лишь только в том случае, когда ее определитель отличен от нуля, то ставится обратная задача: когда не будет обратной матрицы? Для этого надо вычислить определитель данной матрицы и приравнять его к нулю. Получим уравнение первой степени относительно λ , найдя λ его исключаем.

А10. Решить матричное уравнение:
 Пусть
Пусть 
Получим уравнение  . Чтобы найти Х надо обе части равенства умножить слева на обратную матрицу А:
. Чтобы найти Х надо обе части равенства умножить слева на обратную матрицу А:  , т.к.
, т.к.  , то
, то

Найдем обратную матрицу  :
:  обратная матрица существует.
обратная матрица существует. 

А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

Матрица имеет ранг, равный единице, если ее определитель второго порядка равен нулю, т.е. надо вычислить определитель , приравнять его к нулю и найти λ.

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного,элемента какой-либо строки (столбца):
 .
.
Рекомендуем выбрать какой –либо столбец, имеющий элемент -едиицу.
Для данного определителя выберем третий столбец для зануления.
К первой строке прибавим вторую; к третьей строке прибавим вторую, умноженную на три; к четвертой строке прибавим вторую, умноженную на 9.Т.о. получим определитель, где элементы, стоящие в третьем столбце, равны нулю, кроме одного.
 Полученный определитель можно вычислять далее любым способом.
Полученный определитель можно вычислять далее любым способом. 
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.

а) Надо привести определитель к треугольному виду : все элементы расположенные ниже главной диагонали должны быть равны нулю. Для этого элемент  должен быть
должен быть  .Т.к. такого нет, то поменяем местами первый и второй столбцы.
.Т.к. такого нет, то поменяем местами первый и второй столбцы.

В3. Умножить матрицы:
А=  В=
В= 
А×В=С= 
 =1×2+0×3+2×1=4
=1×2+0×3+2×1=4
 =1×7+0×2+2×(-3)=1
=1×7+0×2+2×(-3)=1
 =1×1+0×(-4)+2×5=11
=1×1+0×(-4)+2×5=11
 =0×2+(-1)×3+3×1=0
=0×2+(-1)×3+3×1=0
 =0×7+(-1)×2+3×(-3)=-11
=0×7+(-1)×2+3×(-3)=-11
 =0×1+(-1)×(-4)+3×5=19
=0×1+(-1)×(-4)+3×5=19
 =4×2+0×3+5×1=13
=4×2+0×3+5×1=13
 =4×7+0×2+5×(-3)=13
=4×7+0×2+5×(-3)=13
 =4×1+0×(-4)+5×5=29
=4×1+0×(-4)+5×5=29
А×В=  .
.
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?

Матрицы перестановочны, если А×В= В×А
 =
= 
 =
= 
 =
=  6+5
6+5  =3+
=3+  4
4  = - 3 при
= - 3 при  = -
= -  матрицы А и В перестановочны.
матрицы А и В перестановочны.
В5. Найти обратную матрицу:
А= 
Вычисляем определитель матрицы А:
detA=  =-3≠0, значит, матрица А невырожденная. Находим алгебраические дополнения её элементов:
=-3≠0, значит, матрица А невырожденная. Находим алгебраические дополнения её элементов:
 =
=  =-1,
=-1,  =
=  =-4,
=-4,  =
=  =3,
=3,
 =
=  =-1,
=-1,  =
=  =2,
=2,  =-
=-  =0,
=0,
 =
=  =2,
=2,  =-
=-  =-1,
=-1,  =
=  =-3
=-3
Присоединенная матрица  имеет вид
имеет вид
 =
= 
Следовательно,
 =-
=-  ×
× 
.
В6. Найти ранг матрицы методом Гаусса:
А= 
Приводим матрицу А к ступенчатому виду:






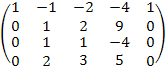


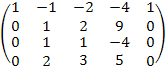




Следовательно, ι (А) = 3.
В7. Решить методом Гаусса систему уравнений:

Составим расширенную матрицу системы и проведем необходимые элементарные преобразования строк:



Последней матрице соответствует система, эквивалентная исходной:
 Отсюда последовательно находим:
Отсюда последовательно находим:  . Система совместна
. Система совместна  и имеет единственное решение.
и имеет единственное решение.
С1. Умножить матрицы:

С2. Решить матричным методом систему уравнений

Найдём определитель матрицы системы
detA=  =-3≠0, значит, к системе применим матричный метод. Находим обратную матрицу
=-3≠0, значит, к системе применим матричный метод. Находим обратную матрицу  :
:
 =-
=- 
Запишем решение системы в матричной форме
 =-
=-  ×
×  =-
=-  =
= 
Следовательно,  =2,
=2,  =-5,
=-5,  =3.
=3.
С3. Решить методом Гаусса системы уравнений:
а)  Преобразуем расширенную матрицу системы:
Преобразуем расширенную матрицу системы:


  (чтобы получить на диагонали элемент, отличный от нуля, приходится изменить порядок неизвестных)
(чтобы получить на диагонали элемент, отличный от нуля, приходится изменить порядок неизвестных)


  Полученной матрице
соответствует система
Полученной матрице
соответствует система
 Система неопределенна (r = 3 < n = 5). Неизвестные
Система неопределенна (r = 3 < n = 5). Неизвестные  , ,  , ,  – базисные, – базисные,  , ,  - свободные. Последовательно находим: - свободные. Последовательно находим:
 = -13 = -13  - 2; - 2;  = -2 = -2  -9 -9  +2=
= -2(-13 +2=
= -2(-13  -2) -9 -2) -9  +2=17 +2=17  +6; +6;
 = =  + 2 + 2  +4 +4  - -  +1=
=17 +1=
=17  +6+2(-13 +6+2(-13  -2)+4 -2)+4  - -  +1=
= -5 +1=
= -5  - -  +3
Полагая +3
Полагая  = u, = u,  = ѵ, получаем общее решение системы в виде = ѵ, получаем общее решение системы в виде
 = -u+5ѵ+3, = -u+5ѵ+3,  =u, =u,  =17ѵ+6, =17ѵ+6,  =13ѵ-2, =13ѵ-2,  = ѵ
б) = ѵ
б)
 Преобразуем расширенную матрицу системы:
Преобразуем расширенную матрицу системы:
 
 

 
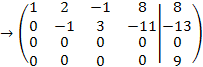 Здесь последовательно выполнили следующие преобразования:
3) Переставили первую и четвертую строки; первую строку, умноженную на 3,2,7, вычли поочередно из второй, третьей, четвертой строк,
4) Вторую строку разделили на 2; вторую строку, умноженную на 1, затем 5, вычли поочередно из третьей, затем четвертой строк.
Последней матрице соответствует система
Здесь последовательно выполнили следующие преобразования:
3) Переставили первую и четвертую строки; первую строку, умноженную на 3,2,7, вычли поочередно из второй, третьей, четвертой строк,
4) Вторую строку разделили на 2; вторую строку, умноженную на 1, затем 5, вычли поочередно из третьей, затем четвертой строк.
Последней матрице соответствует система
 (Уравнение 0=0, соответствующее третьей строке матрицы, отброшено). Мы пришли к системе, содержащей противоречивое уравнение 0=9. Ранги основной матрицы системы и расширенной матрицы не равны. Система несовместима.
(Уравнение 0=0, соответствующее третьей строке матрицы, отброшено). Мы пришли к системе, содержащей противоречивое уравнение 0=9. Ранги основной матрицы системы и расширенной матрицы не равны. Система несовместима.
| |
в)  .
Однородная система всегда имеет решение. Если определитель основной матрицы системы равен нулю, то система имеет множество решений. Если же определитель не равен нулю, то система имеет единственное нулевое решение.
С помощью элементарных преобразований получим: .
Однородная система всегда имеет решение. Если определитель основной матрицы системы равен нулю, то система имеет множество решений. Если же определитель не равен нулю, то система имеет единственное нулевое решение.
С помощью элементарных преобразований получим: 
|
Будем считать базисными переменными  , а свободными
, а свободными  . Имеем систему
. Имеем систему
 Отсюда получим решение:
Отсюда получим решение:

ЛИТЕРАТУРА
1.Шипачев, Виктор Семенович. Высшая математика : [учеб. для вузов] / В. С. Шипачев. - Изд. 8-е, стер. - М. : Высш. шк., 2007. - 479 с.
2.Зайцев, Владимир Петрович. Математика : учеб. пособие / В. П. Зайцев ; Алт. гос. техн. ун-т им. И. И. Ползунова, [Ин-т интенсив. образования]. - Барнаул : Изд-во АлтГТУ, 2007 - Ч. 1. - 2007. - 242 с
3.Высшая математика в упражнениях и задачах : в 2 ч. / П. Е. Данко [и др.]. - 6-е изд. - М. : Оникс : Мир и Образование, 2007 - . - На обл. указаны авт.: П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Ч. 1. - 2007. - 304 с.
4.Высшая математика для экономических специальностей : учеб. и практикум, части I и II; под ред. Н. Ш. Кремера. - 2-е изд., перераб. и доп. - М. : Высш. образование, 2007. - 893 с. : ил.
5.Высшая математика для экономических специальностей : учеб. и практикум, части I и II : / Кремер Н. Ш. и др.] ; Под ред. Н. Ш. Кремера. - 2-е изд., перераб. и доп. - М. : Высш. образование, 2008. - 893 с. :
6.Шипачев, Виктор Семенович. Курс высшей математики : учеб. для вузов / В. С. Шипачев ; под ред. А. Н. Тихонова. - 3-е изд., испр. - М. : ОНИКС, 2007. - 599 с. : ил.
7.Попов, Максим Александрович. Высшая математика для студентов технических вузов : ответы на экзаменац. вопр. : учеб. пособие / М. А. Попов. - М. : Экзамен, 2007. - 252 с.
8.Высшая математика в упражнениях и задачах : в 2 ч. / П. Е. Данко [и др.]. - 7-е изд., испр. - М. : Оникс : Мир и Образование, 2008 Ч. 1. - печ. 2008. - 368 с. : ил.
9.Минорский, Василий Павлович. Сборник задач по высшей математике / В. П. Минорский. - Изд. 15-е. - М. : Физматлит, 2008. - 336 с. : ил.
10.Соболь, Борис Владимирович. Практикум по высшей математике / Б. В. Соболь, Н. Т. Мишняков, В. М. Поркшеян. - Изд. 4-е. - Ростов н/Д : Феникс, 2007. - 630 с. - (Высшее образование).
Людмила Михайловна Кобзарь
Екатерина Владимировна Мартынова
Валентина Михайловна Кайгородова
Издано в авторской редакции.
Подписано в печать
Формат 60x84 1/16
Печать - ризография. Усл.п.л. 1,63.
Тираж 100 экз. Заказ 2008
Издательство Алтайского государственного технического университета им. И.И. Ползунова,
656099, г.Барнаул, пр-т Ленина, 46
Лицензия на издательскую деятельность
ЛР№020822 от 21.09.98 г.
Отпечатано в типографии АлтГТУ
Лицензия на полиграфическую деятельность
ПЛД №28-35 от 15.07.97 г.
| <== previous lecture | | | next lecture ==> |
| Метод Гаусса. | | | ЗАПРОШЕННЯ |