Запись и решение системы линейных алгебраических уравнений в линейном виде.

Date: 2015-10-07; view: 374.

Неизвестные или переменные уравнений общепринято обозначать буквами х₁, х₂,… х_n. Уравнение называется линейным относительно переменных х₁, х₂,… х_n, если оно записано в виде .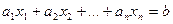

Здесь 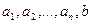– произвольные действительные числа.

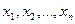Набор чисел называется решением уравнения, если в результате подстановки этих чисел вместо неизвестных уравнение превращается в алгебраическое тождество

.

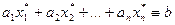Пусть задана совокупность уравнений. В общем виде такая система уравнений записывается так:

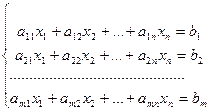
В общем виде система уравнений содержит m уравнений и n неизвестных. Коэффициенты при неизвестных имеют два индекса – первый индекс указывает номер уравнения, а второй – номер неизвестной. Коэффициенты b₁, b₂, …b_m, называются свободными элементами уравнений.