Решение системы линейных алгебраических уравнений методом Гаусса.

Date: 2015-10-07; view: 380.

Метод Гаусса называют методом последовательного исключения неизвестных. Сущность метода заключается в том, что при помощи элементарных преобразований, таких как умножения (деления) любого уравнения системы на число и сложения с любым другим уравнением система приводится к треугольному виду. Последнее уравнение позволяет сделать заключение о совместности системы и, если система определенна, найти одно из неизвестных. Затем, двигаясь от последнего уравнения к первому (операции обратного хода), последовательно определяются все неизвестные системы.

Рассмотрим алгоритм метода Гаусса на примере решения системы уравнений.

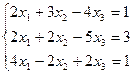
В рассматриваемом примере коэффициенты при всех неизвестных отличны от единицы. Сделаем первое уравнение ведущим для исключения переменной х₁, для чего все уравнение разделим на коэффициент при х₁, который равен 2.

Ведущее уравнение запишем первым в системе

Из системы уравнений видно, что для исключения неизвестной х₁ из второго уравнения нужно первое уравнение умножить на (-2) и сложить со вторым. Для исключения неизвестной х₁ из третьего уравнения нужно первое уравнение умножить на (-4) и сложить с третьим.

В результате этих операций система уравнений будет иметь вид:

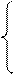
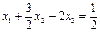
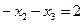
Теперь за ведущее примем второе уравнение и исключим неизвестную х₂ из третьего уравнения. Для этого второе уравнение нужно умножить на (-8) и сложить с третьим.

Будем иметь систему уравнений

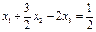
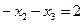
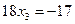
Это были операции прямого хода. В результате исключения неизвестных х₁ и х₂ получена система треугольного вида.

Операции обратного хода.

Из последнего уравнения определяется ;

Из второго уравнения определяется ;

Из первого уравнения определяется .