
Вычисление обратной матрицы методом Гаусса.
Date: 2015-10-07; view: 411.
Вычисление обратной матрицы методом Гаусса заключается в том, что любую неособенную матрицу А путем элементарных преобразований только столбцов (или только строк) можно привести к единичной матрице Е, и если совершенные над матрицей А элементарные преобразования в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать элементарные преобразования над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. При отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример. Методом исключения Гаусса найдем матрицу, обратную к матрице
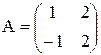
Решение:
К матрице А справа приписывается единичная матрица того же порядка (А|E)
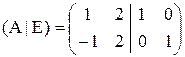
Матрица (А|E) приводится элементарными преобразованиями первого и второго типов к ступенчатому виду
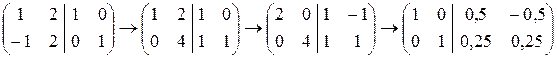
| <== previous lecture | | | next lecture ==> |
| Решение системы линейных алгебраических уравнений методом Гаусса. | | | Системы линейных однородных уравнений. Свойства. Фундаментальное решение. |