Системы линейных однородных уравнений. Свойства. Фундаментальное решение.

Date: 2015-10-07; view: 360.

В общем виде система n линейных однородных алгебраических уравнений запишется

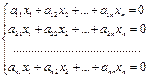
Очевидно, такая система имеет нулевое (тривиальное) решение

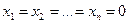
Если ∆ ≠ 0, то такая система имеет единственное решение, корни которого 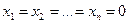. Других ненулевых решений нет.

Если ∆ = 0, то так как все вспомогательные определители системы равны нулю, то система имеет бесконечное множество решений.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

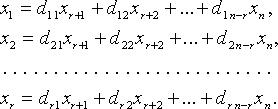
Тогда n - r линейно независимыми вектор-решениями будут:

а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.