
Общее решение системы линейных алгебраических уравнений. Свободные неизвестные. Базисные решения.
Date: 2015-10-07; view: 406.
Рассмотрим однородную линейную систему
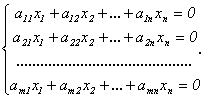
Отметим, что такая система всегда совместна, поскольку имеет нулевое решение 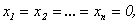 называемое тривиальным.
называемое тривиальным.
Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся m – r уравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первые r уравнений:
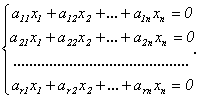
Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:
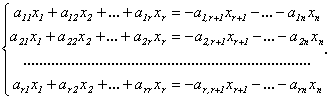
Эта система будет иметь единственное решение относительно неизвестных 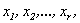 выражающее их через остальные неизвестные (
выражающее их через остальные неизвестные ( 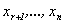 ), которым можно придавать любые произвольные значения. Таким образом, система при r<n является неопределенной.
), которым можно придавать любые произвольные значения. Таким образом, система при r<n является неопределенной.
Неизвестные 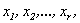 коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (
коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные ( 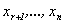 ) –свободными неизвестными.
) –свободными неизвестными.
Решения системы  называются линейно независимыми, если линейная комбинация
называются линейно независимыми, если линейная комбинация  дает нулевой столбец только при
дает нулевой столбец только при 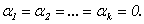
| <== previous lecture | | | next lecture ==> |
| Системы линейных однородных уравнений. Свойства. Фундаментальное решение. | | | Модель многоотраслевой экономики Леонтьева. |