
Модель многоотраслевой экономики Леонтьева.
Date: 2015-10-07; view: 404.
Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Введем следующие обозначения:
xi - общий (валовой) объем продукции i-й отрасли (i = 1,2,...,n);
xij - объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства (i,j = 1,2,...,n);
yi - объем конечного продукта i-й отрасли для непроизводственного потребления.
Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями и конечного продукта, то
xi = (xi1 + xi2+ ... + xin) + yi , (i = 1,2,...,n).
Эти уравнения (их n штук) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в эти уравнения, имеют стоимостное выражение.
Введем коэффициенты прямых затрат:
aij = xij / xj , (i,j = 1,2,...,n),
показывающие затраты продукции i-й отрасли на производство единицы стоимости j-й отрасли.
Можно полагать, что в некотором промежутке времени коэффициенты aij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
xij = aijxj , (i,j = 1,2,...,n),
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.
Теперь соотношения баланса примут вид:
xi = (ai1x1 + ai2x2 + ... + ainxn) + yi , (i = 1,2,...,n),
Обозначим
 ,
, 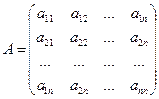 ,
, 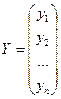 ,
,
где
X- вектор валового выпуска;
A - матрица прямых затрат (технологическая или структурная матрица);
Y - вектор конечного продукта.
Тогда соотношения баланса можно записать в виде:
X = AX + Y.
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат Aобеспечивает заданный вектор конечного продукта Y.
Перепишем матричное уравнение в виде:
(E - A) X = Y.
Если матрица (E - A)невырожденная, т.е. ее определитель не равен нулю, тогда:
X = (E - A)-1 Y.
Матрица S = (E - A)-1 называется матрицей полных затрат.
Чтобы выяснить экономический смысл элементов матрицы S = (sij), будем задаваться единичными векторами конечного продукта:
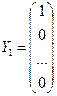 ,
, 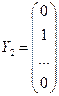 , …,
, …, 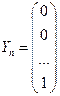 .
.
Тогда соответствующие векторы валового выпуска будут:
 ,
, 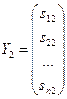 , …,
, …,  .
.
Следовательно, каждый элемент sij матрицы Sесть величина валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли.
В соответствии с экономическим смыслом задачи значения xi должны быть неотрицательны при неотрицательных значениях yi и aij.
Матрица Аназывается продуктивной, если для любого вектора Y существует решение X уравнения (E - A) X = Y. В этом случае и модель Леонтьева называется продуктивной.
| <== previous lecture | | | next lecture ==> |
| Общее решение системы линейных алгебраических уравнений. Свободные неизвестные. Базисные решения. | | | Линейное пространство. |