Базис линейного пространства. Размерность линейного пространства.

Date: 2015-10-07; view: 412.

Базисом линейного пространства L называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов.

В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

Линейное пространство L , в котором существует базис, состоящий из n векторов, называется n -мерным линейным или векторным пространством. Число n называется размерностью пространства и обозначается dimL. Линейное пространство, в котором не существует базис, называется бесконечномерным.

19. Преобразование координат при переходе к новому базису.

Рассмотрим линейное преобразование А и два базиса в трехмерном пространстве: е₁, е₂, е₃ и е₁, е₂, е_3. Пусть матрица С задает формулы перехода от базиса {e_k} к базису {e_k}. Если в первом из этих базисов выбранное линейное преобразование задается матрицей А, а во втором – матрицей А, то можно найти связь между этими матрицами, а именно:

А = С^-1АС

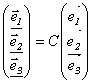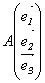Действительно, , тогда А . С другой стороны, результаты применения одного и того же линейного преобразования А в базисе {e_k}, т.е. , и в базисе {e_k}: соответственно 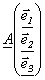- связаны матрицей С: 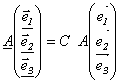, откуда следует, что СА=АС. Умножая обе части этого равенства слева на С^-1, получим С^-1СА = = С^-1АС, что доказывает справедливость формулы.