
Скалярное произведение векторов. Угол между векторами.
Date: 2015-10-07; view: 385.
Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:
ab = |a||b| cosφ .
Обозначения скалярного произведения: ab, (ab), a·b .
Свойства скалярного произведения:
1. ab = |a| праb.
Доказательство. По свойству проекции праb = |b| cosφ, следовательно, ab = |a| праb.
2. ab = 0 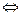 a
a  b.
b.
3. ab = ba .
4. (ka)b = k(ab).
5. (a + b)c = ac + bc .
6. a2 = aa = |a|2 , где а2 называется скалярным квадратом вектора а.
7. Если векторы а и b определены своими декартовыми координатами
a = {X1, Y1, Z1}, b = {X2, Y2, Z2},
то ab = X1X2 + Y1Y2 + Z1Z2.
Доказательство. Используя формулу, получим:
ab = (X1i + Y1j + Z1k)(X2i + Y2j + Z2k) .
Используя свойства 4 и 5, раскроем скобки в правой части полученного равенства:
ab = X1X2ii +Y1Y2jj + Z1Z2kk + X1Y2ij +X1Z2ik + Y1X2ji + Y1Z2jk + Z1X2ki + Z1Y2kj.
Но ii = jj = kk = 1 по свойству 6, ij = ji = ik = ki = jk = kj = 0 по свойству 2, поэтому
ab = X1X2 + Y1Y2 + Z1Z2 .
Угол между векторами:
cosφ = 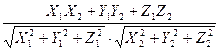 .
.
| <== previous lecture | | | next lecture ==> |
| Базис линейного пространства. Размерность линейного пространства. | | | Линейные преобразования. Свойства. |