
Линейные преобразования. Свойства.
Date: 2015-10-07; view: 404.
Ортонормированный базис. Евклидово пространство.
Если векторы e1, e2, e3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x1, x2, x3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R3 выбрана правая система декартовых прямоугольных координат {0, i, j, k}.
Ортонормированная система, состоящая из n векторов n-мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.
Если e1, e2, ..., en — ортонормированный базис n-мерного евклидова пространства и
x = x1e1 + x2e2 + ... + xnen — разложение вектора x по этому базису, то координаты xi вектора xв ортонормированном базисе вычисляются по формулам xi =(x, ei),i = 1, 2, ..., n.
Евклидово пространство (также Эвклидово пространство) — в изначальном смысле, пространство свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
Ортогональные операторы
Линейный оператор 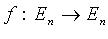 называется ортогональным, если
называется ортогональным, если
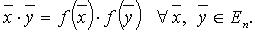
Для того чтобы оператор 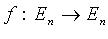 был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.
был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.
Ортогональные операторы и только они сохраняют длину вектора, т. е.

Сопряженные операторы
Оператор 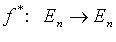 называется сопряженным линейному оператору
называется сопряженным линейному оператору 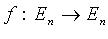 , если
, если
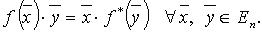
Оператор 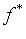 также является линейным оператором. Если f в некотором ортогональном базисе имеет матрицу A, то в этом базисе оператор
также является линейным оператором. Если f в некотором ортогональном базисе имеет матрицу A, то в этом базисе оператор 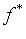 имеет матрицу
имеет матрицу 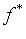 .
.
Свойства сопряженных операторов: 
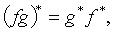


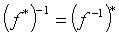 (f - невырожденный).
(f - невырожденный).
Самосопряженные операторы
Линейный оператор 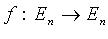 называется самосопряженным (симметрическим), если
называется самосопряженным (симметрическим), если

Для самосопряженного оператора 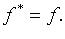
Оператор 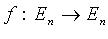 является самосопряженным тогда и только тогда, когда его матрица в некотором ортонормированном базисе симметрическая.
является самосопряженным тогда и только тогда, когда его матрица в некотором ортонормированном базисе симметрическая.
Свойства самосопряженных операторов: 1) самосопряженный оператор имеет только действительные собственные числа; 2) всякий самосопряженный оператор является оператором простой структуры; 3) для всякого самосопряженного оператора существует ортонормированный базис, состоящий из собственных векторов этого оператора.
23. Нахождение матрицы линейного преобразования.
Пусть в n- мерном линейном пространстве с базисом 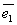 ,
, 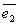 ,…,
,…, 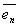 задано линейное преобразование А. Тогда векторы А
задано линейное преобразование А. Тогда векторы А 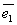 ,А
,А 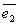 ,…,А
,…,А 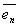 - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
A 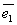 = a11
= a11 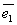 + a21
+ a21 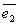 +…+ an1
+…+ an1 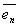
A 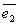 = a12
= a12 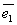 + a22
+ a22 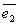 +…+ an2
+…+ an2 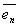
……………………………….
A 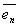 = an1
= an1 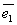 + an2
+ an2 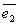 +…+ ann
+…+ ann 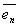
Тогда матрица А =  называется матрицей линейного преобразования А.
называется матрицей линейного преобразования А.
Если в пространстве L взять вектор 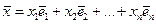 , то A
, то A 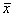 Î L.
Î L.
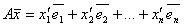 , где
, где

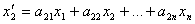
……………………………..
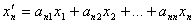
Эти равенства можно назвать линейным преобразованием в базисе 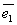 ,
, 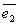 ,…,
,…, 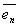 .
.
В матричном виде:
 , А×
, А× 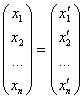 ,
, 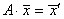
| <== previous lecture | | | next lecture ==> |
| Скалярное произведение векторов. Угол между векторами. | | | Ранг и дефект линейного преобразования. |