
Ранг и дефект линейного преобразования.
Date: 2015-10-07; view: 500.
Пусть A — матрица размера 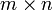 над полем C (или R). Пусть T — линейное преобразование, соответствующее A в стандартном базисе; это значит, что T(x) = Ax. Ранг матрицы A — это размерность области значений преобразования T.
над полем C (или R). Пусть T — линейное преобразование, соответствующее A в стандартном базисе; это значит, что T(x) = Ax. Ранг матрицы A — это размерность области значений преобразования T.
Ядро оператора: 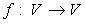 - множество, обозначаемое Ker f:
- множество, обозначаемое Ker f:
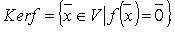
Область значений (образ) оператора 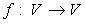 - множество, обозначаемое Im f:
- множество, обозначаемое Im f:
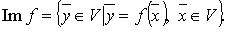
Множества Ker f и Im f являются подпространствами пространства V.
Ранг оператора  (обозначение: dim Im f) - ранг матрицы A линейного оператора f,
(обозначение: dim Im f) - ранг матрицы A линейного оператора f,
dim Im f = rank A.
Дефектом оператора  называют dim Ker f,
называют dim Ker f,
dim Im f + dim Ker f = n.
 25. Определение, геометрическая интерпретация и формы записи комплексного числа.
25. Определение, геометрическая интерпретация и формы записи комплексного числа.
Комплексным числом z будем называть упорядоченную пару действительных чисел x, y записанную в форме z = x + iy, где i- новый объект ("мнимая единица"), для которого при вычислениях полагаем i2 = -1.
Первая компонента комплексного числа z, действительное число x, называется действительной частью числа z, это обозначается так: x = Re z; вторая компонента, действительное число y, называется мнимой частью числа z: xy = Im z.
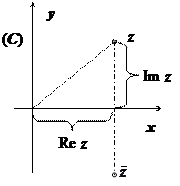
Геометрически комплексное число z = x + iy изображается как точка с координатами ( x, y) на плоскости. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью С.
Тригонометрическая форма комплексного числа. Запись комплексного числа в виде z = x + iy называется алгебраической формой комплексного числа. Изобразим число z как точку на плоскости с декартовыми координатами x, y. Если теперь перейти к полярным координатам  , то
, то 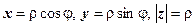 , поэтому
, поэтому 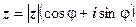 . Угол
. Угол  называется аргументом комплексного числа z и обозначается
называется аргументом комплексного числа z и обозначается 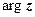 :
:  . Аргумент комплексного числа определён неоднозначно (с точностью до слагаемых, кратных
. Аргумент комплексного числа определён неоднозначно (с точностью до слагаемых, кратных  ): если, например,
): если, например, 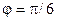 , то значения
, то значения  , равные
, равные 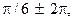
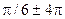 и т.д. тоже будут соответствовать числу z; значение аргумента, удовлетворяющее условиям
и т.д. тоже будут соответствовать числу z; значение аргумента, удовлетворяющее условиям 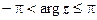 , называют главным; для обозначения всех значений аргумента комплексного числа z применяется символ
, называют главным; для обозначения всех значений аргумента комплексного числа z применяется символ  :
: 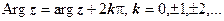 .
.
Показательная форма комплексного числа. Ряд Маклорена для функции 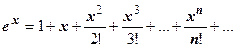 сходится к функции при любом действительном х. Формально запишем это разложение для
сходится к функции при любом действительном х. Формально запишем это разложение для 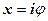 :
: 
Степени числа i: i 2 = -1; i 3 = i 2 i = - i ; i 4 = i 2 i 2 = 1 ; i 5 = i 4 i = i ; i 6 = i 2 = -1; далее значения степеней повторяются (для отрицательных степеней это тоже справедливо: i -1 = - i ; i - 2 = -1; i - 3 = i ; i -4 = 1 ; и т.д.). Поэтому 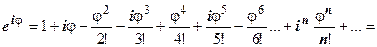
 . В круглых скобках стоят ряды для
. В круглых скобках стоят ряды для 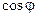 и
и 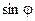 , которые сходятся для любого действительного
, которые сходятся для любого действительного  ; поэтому получаем
; поэтому получаем  . Эта формула называется формулой Эйлера. Теперь любое комплексное число
. Эта формула называется формулой Эйлера. Теперь любое комплексное число 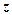 можно представить как
можно представить как 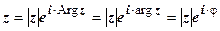 ; эта форма записи называется показательной.
; эта форма записи называется показательной.
26. Операции над комплексными числами.
Два комплексных числа z1 = x1 + iy1 и z2 = x2 + iy2 равны тогда и только тогда, когда равны их действительные и мнимые части: 
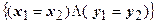 .
.
Множество комплексных чисел неупорядочено, т.е. для комплексных чисел не вводятся отношения "больше" или "меньше".
Суммой двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число z, определяемое соотношением z =(x1 + x2) + (y1 + y2) i, т.е. Re(z1 + z2) = Re z1 + Re z2, Im(z1 + z2) = Im z1 + Im z2.
Это означает, что геометрически комплексные числа складываются как векторы на плоскости, покоординатно.
Произведением двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число z, определяемое соотношением z = (x1x2 - y1y2) + (x1y2 + x2y1) i, т.е.
Re(z1 z2) = Re z1 Re z2 – Im z1 Im z2; Im(z1 z2) = Re z1 Im z2 + Im z1 Re z2.
Для нахождения частного комплексных чисел  домножим числитель и знаменатель на число, сопряжённое знаменателю:
домножим числитель и знаменатель на число, сопряжённое знаменателю: 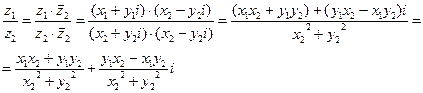 .
.
| <== previous lecture | | | next lecture ==> |
| Линейные преобразования. Свойства. | | | Собственные значения и собственные векторы матриц, свойства собственных векторов. |