Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя.

Date: 2015-10-07; view: 467.

1/2

B(-13, -17)

164. Find the length of the minor axis of the ellipse with center (0,0), foci (0,±3) and vertex (0,5).

b=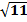

165. Find equation of a circle which center C(2,-3) and radius is R=6.

166. Let A (4,6) , B (4,0) , C (1,4) be vertices of the triangle. Find the equation of side AB.

6x-8y+24=0

167. Let A (4,6) , B (4,0) , C (1,4) be vertices of the triangle. Find the equation of side BC.

3y+4y+16=0

168. Let A (4,6) , B (4,0) , C (1,4) be vertices of the triangle. Find the equation of the height

from vertex A .

4y-3y+2=0

169. Let A (4,6) , B (4,0) , C (1,4) be vertices of the triangle. Find equation of the median

dropped from vertex C.

y-7y-3=0

170. Find equation of the straight line through the point A(-1,-3) if the angle between it and the

Y-axis is 450.

171. Find equation of the straight line through the point A(-1,-3) if the angle between it and the эти три примера лучше перерешать)))

Y-axis is 300.

172. Find equation of the straight line through the point A(-1,-3) if the angle between it and the

Y-axis is 1800.

173. Two points A(3,1), B(3,7) are given. Find coordinates of point M on Y-axis such that

straight lines AM and BM are mutually perpendicular.

Y=22

174. Find distance from the origin to the straight line: 9x 12y 10 0.

D=2/3

175. Find angle between straight lines 2x y 5 0 and 6x 2y 7 0 .

45

176. Find distance from the origin to the straight line x-y=0.

D=0

177. Determine a so that the lines 3ax 8y 13 0 and (a 1)x 2ay 21 0 are parallel.

a1=2; a2= -2/3

178. Find the equation of the straight line through the point P(5,2) and perpendicular to the

straight line 4x y 3 0 .

x+4y+18=0

179. Find equation of the plane that passed through the point (2,5,3) and is parallel to the

coordinate plane XOZ.

x+z-5=0

180. Find equation of the plane through the three points M1(1, 2, -1); M2(-1, 0 , 4); M3(-2, -1, 1).

11x-11y+12z+23=0

181. Find equation of the plane through point A(1,2-4) and is parallel to the XOY-plane.

X+y-3=0

182. Find distance between two parallel planes: 5x + 3y - 4z + 15 = 0; 15x + 9y - 12z - 5 = 0.

D=-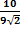

183. Find distance between two parallel planes: 11x 2y 10z 15 0, 11x 2y 10z 45 0.

D=-4

184. Find the volume of the tetrahedron if its vertices are A(0,0,2), B(3,0,5), C(1,1,0), D(4,1,2) .

185. Coordinates of vertices of triangle ABC are A(1,6), B(-5,4), C(2,-3). Find angle at vertex B.

Arccos(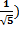

186. Find angle between the line 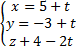and the plane 4x-2y-2z+7=0.

60

187. Find the angle between the planes 3y-z=0 and 2y-z=0.

Arccos( )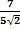

188. Find canonical equation of the line x y z 2 0, x 2y z 4 0.

189. Find equation of the line through point M(5,-2) and parallel to the OY-axis.

X=5

190. In the triangle ABC find length of the altitude (height) AH if: A(1,-8), B(7,2), C(-5,2)

191. Find equation of the plane through the point (2,-1,5) and parallel to the plane x-3y+5z-1=0.

x-3y+5z-24=0

192. Find equation of the plane passing through the point (2,5,3) and is parallel to the coordinate

plane XOY.

X+Y-7=0

193. Find point of intersection of straight line 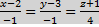and plane x 2y 3z 14 0.

M(1,2,3)

194. Find area of the parallelogram formed by vectors a and b: a p 2q , b 3p q; Тупо не знаем как решать XD

p 1, q 2, ( p^ q) / 6.

195. Find area of the parallelogram formed by vectors a and b: a 3p q , b p 2q;

p 4, q 1, ( p^ q) / 4.

196. Find area of the parallelogram formed by vectors a and b: a 10p q , b 3p 2q;

p 4, q 1, ( p^ q) / 6.

-46 ß вроде как))))

197. Find canonical equation of the line passing through point M(1,0,-2) and parallel to the vector

s 2i 3 j .

2x-3y-1=0 and Not my answer: x=1

198. Find angle between straight lines 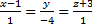And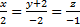

45

199. Find the values of α and β such that vector a (3,1,) is perpendicular to the vector

b (2,,1) if b 3.

a=-4 and not my answer: a=-8

200. Find distance between two points A(5,2) and B(3,-3).

D=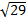

Определитель (детерминант) – число, которое ставится в соответствие квадратной таблице чисел по определенным правилам.

Определитель второго порядка: = =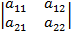

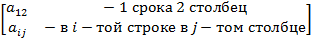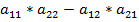
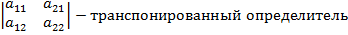
При транспонировании определитель не меняется.

Определитель = 0, когда: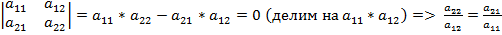

или 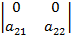=0

Определитель 3-го порядка -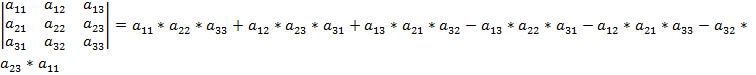

или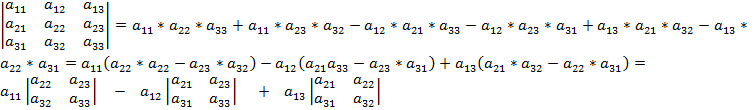

(минор 1 элемента) (минор 2 элемента) (минор 3 элемента)

Если минор домножить на «-», то он становится алгебраическим дополнением.

A_ij=M_ij*(-1)^i+j

Определитель n-ого порядка: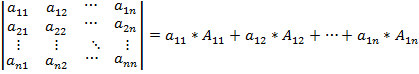

Свойства:

1) При транспонировании определитель не меняется.

2) При перестановке любых 2 строк(столбцов) определитель меняет знак.

3) Если в определителе 2 строки (столбца) одинаковы, то определитель = 0.

4) Если какая либо строка или столбец состоит только из 0, то определитель = 0.

5) Если в определителе 2 строки или 2 столбца пропорциональны, то определитель = 0.

6) Число, умноженное на определитель = определителю у которого одна строка или столбец умножена на это число.

7) Пусть 2 определителя отличаются только 2 строками, тогда сумма определителя = определителю, у которого одинаковые строки остаются, а не одинаковые складываются.
Пример:

8) Если какая то строка является линейной комбинацией остальных строк, то определитель = 0.

9) Если в какой-либо строке добавить линейную комбинацию каких-нибудь других строк, то определитель не меняется.

10) Определитель = сумме произведений элементов какой-либо одной строки на их алгебраическое дополнение.

11) Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю.

12) Определитель = 0, ó какая-либо строка является линейной комбинацией другой строки.

Будем говорить, что некоторая строка (а₁, a₂, ..., а_n) является линейной комбинацией строк (b₁, b₂, ...,b_n), (c₁ c₂, ..., c_n), .... (d₁ d₂, .... d_n) с коэффициентами λ, μ, ...,ν, если а_j= λb_j + μc_j + ... + νd_j для всех j— 1, 2, .... n.