
ТЕМА 3. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Date: 2015-10-07; view: 499.
Контрольные задания
2.1-2.20. Решить систему методом Жордана-Гаусса. Найти общее решение и два частных решения. Сделать проверку.
2.1. 2.2.


2.3. 2.4.


2.5. 2.6.


2.7. 2.8.


2.9. 2.10.

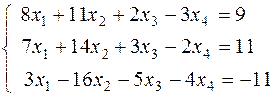
2.11. 2.12.


2.13. 2.14.


2.15. 2.16.


2.17. 2.18.


2.19. 2.20.


Пусть на интервале  задана функция
задана функция  . Возьмем некоторое число
. Возьмем некоторое число  и придадим аргументу
и придадим аргументу  приращение
приращение  . Тогда значение функции получит приращение
. Тогда значение функции получит приращение  . Рассмотрим отношение
. Рассмотрим отношение 
 . Если при
. Если при  существует конечный предел дроби
существует конечный предел дроби  , то этот предел называют произвoдной функции
, то этот предел называют произвoдной функции  в точке
в точке  и обозначают символом
и обозначают символом  (или
(или  ):
):
 .
.
Нахождение производной называют дифференцированием функции.
Функцию  называют дифференцируемой в точке
называют дифференцируемой в точке  , если в окрестности этой точки ее приращение может быть представлено в виде:
, если в окрестности этой точки ее приращение может быть представлено в виде:

 .
.
Можно доказать, что для дифференцируемости функции необходимо и достаточно, чтобы существовала и была конечной ее производная, при этом  .
.
Выражение  называют дифферен-циалом функции и обозначают
называют дифферен-циалом функции и обозначают  . Приращение аргумента
. Приращение аргумента  называют дифференциалом независимой переменной и обозначают
называют дифференциалом независимой переменной и обозначают  . Таким образом,
. Таким образом,  .
.
Геометрически дифференциал  есть приращение касательной, проведенной к графику функции в точке
есть приращение касательной, проведенной к графику функции в точке  , и может быть как меньше, так и больше приращения функции
, и может быть как меньше, так и больше приращения функции  . Для линейной функции
. Для линейной функции 

Если производная существует для всех  из интервала
из интервала  , то тем самым производная определена как функция
, то тем самым производная определена как функция  в этом интервале, и можно говорить о производной от этой функции, называемой второй производной функции
в этом интервале, и можно говорить о производной от этой функции, называемой второй производной функции  :
:  Аналогично вводится понятие высших производных (третья производная и т.д.)
Аналогично вводится понятие высших производных (третья производная и т.д.) 
Для освоения техники дифференцирования, то есть нахождения производных, необходимо использовать правила дифференцирования и таблицу производных наиболее часто встречающихся функций.
Основные правила дифференцирования
1. 
 .
.
2.  (
(  – постоянная)
– постоянная)  .
.
3. 

4. 
 .
.
5. Производная сложной функции: если 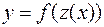 , то
, то  , где производные функций в правой части равенства берутся по аргументам
, где производные функций в правой части равенства берутся по аргументам  и
и  соответственно.
соответственно.
Приведем таблицу производных наиболее часто используемых функций:
1.  (
(  – постоянная)
– постоянная) 
2. 

3. 

4.  (
(  – постоянная)
– постоянная) 
5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Логарифмической производной функции  называется производная от логарифма этой функции:
называется производная от логарифма этой функции:  , при y > 0. Нахождение производных от многих функций значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. При этом логарифмическую производную применяют формально, не учитывая, что формула имеет смысл лишь при y > 0.
, при y > 0. Нахождение производных от многих функций значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. При этом логарифмическую производную применяют формально, не учитывая, что формула имеет смысл лишь при y > 0.
Функция y(x) называется неявной, если зависимость между х и у выражена уравнением F(x,y)=0, неразрешенным относительно у.
Чтобы найти производную от неявной функции, надо данное уравнение продифференцировать, считая у функцией от х, а затем полученное уравнение решить относительно производной  .
.
Рассмотрим примеры вычисления производных.
Пример1. Найти производную функции  .
.
Решение. Применяя правила 4,1 и таблицу производных, получим:
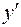

 .
.
Пример2. Найти  , если
, если  .
.
Решение. Последовательно применяя правило дифференцирования сложной функции, получим:


Пример3. Найти производную функции  .
.
Решение. Применим логарифмическую производную:

Пример4. Найти производную функции  .
.
Решение. В случае произведения нескольких сомножителей применение логарифмической производной также эффективно:


 .
.
Пример5. Найти производную функции  , если
, если  .
.
Решение. Применим правило дифференцирования неявной функции:



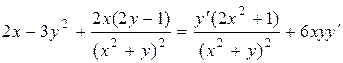


Функция  называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале  , полностью входящем в область ее определения, если для любых
, полностью входящем в область ее определения, если для любых  и
и  из этого интервала из неравенства
из этого интервала из неравенства  следует выполнение неравенства
следует выполнение неравенства  (
(  ). Если неравенства выполняются как строгие, то говорят о строгом возрастании (убывании) функции. Интервалы, на которых функция возрастает или убывает, называются интервалами монотонности функции.
). Если неравенства выполняются как строгие, то говорят о строгом возрастании (убывании) функции. Интервалы, на которых функция возрастает или убывает, называются интервалами монотонности функции.
Внутренняя точка  интервала
интервала  называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если существует такое
, если существует такое  , что для всех
, что для всех  из интервала
из интервала  , содержащегося внутри интервала
, содержащегося внутри интервала  , выполняется неравенство
, выполняется неравенство  (
(  ). Точки максимума и минимума называют точками экстремума функции.
). Точки максимума и минимума называют точками экстремума функции.
Приведем формулировки теорем, используемых при исследовании функций.
Достаточное условие строгого возрастания (убывания) функции.
Если  (
(  ) в интервале
) в интервале  , то
, то  строго возрастает (убывает) в этом интервале.
строго возрастает (убывает) в этом интервале.
Необходимое условие экстремума функции.
Если функция  дифференцируема в точке
дифференцируема в точке  и достигает в этой точке максимума (минимума), то
и достигает в этой точке максимума (минимума), то  .
.
Точками экстремума могут быть только точки, в которых производная равна нулю, либо производная не существует. Точки, в которых производная равна нулю или не существует, называют точками, подозрительными на экстремум, или критическими точками.
Достаточное условие экстремума функции.
Если при переходе через точку  , подозрительную на экстремум, производная меняет знак, то точка
, подозрительную на экстремум, производная меняет знак, то точка  является точкой экстремума. При этом если в некоторой окрестности точки
является точкой экстремума. При этом если в некоторой окрестности точки 
 для
для  и
и 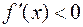 для
для  , то
, то  является точкой максимума. Если же в этой окрестности
является точкой максимума. Если же в этой окрестности 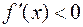 для
для  и
и  для
для  , то
, то  – точка минимума.
– точка минимума.
При исследовании функции на экстремум рекомендуется придерживаться следующего плана.
1. Найти область определения функции.
2. Найти производную функции.
3. Найти корни производной  и точки ее разрыва, принадлежащие области определения функции (то есть точки, подозрительные на экстремум).
и точки ее разрыва, принадлежащие области определения функции (то есть точки, подозрительные на экстремум).
4. Определить интервалы знакопостоянства производной, границами которых служат точки, подозрительные на экстремум.
5. Определить знак производной на каждом из образовавшихся интервалов. Если при переходе через точку, подозрительную на экстремум, производная меняет знак с плюса на минус (с минуса на плюс), то эта точка – точка максимума (минимума). Если же при переходе через точку, подозрительную на экстремум, производная знака не меняет, то экстремума в этой точке нет.
Пример 6. Найти область определения и экстремумы функции  .
.
| <== previous lecture | | | next lecture ==> |
| ТЕМА 2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ | | | Решение. |