
Необходимость
Date: 2015-10-07; view: 396.
Доказательство
Теорема Кронекера - Капелли
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных.
Пусть система совместна. Тогда существуют числа 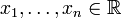 такие, что
такие, что 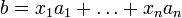 . Следовательно, столбец b является линейной комбинацией столбцов
. Следовательно, столбец b является линейной комбинацией столбцов 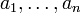 матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк вычеркнуть или приписать строку, которая является линейной комбинацией других строк следует, что
матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк вычеркнуть или приписать строку, которая является линейной комбинацией других строк следует, что 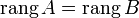 .
.
| <== previous lecture | | | next lecture ==> |
| Метод Гаусса .Элементарные преобразования матрицы | | | Достаточность |