
Линейные операции над векторами. Свойства.
Date: 2015-10-07; view: 483.
Линейными операциями над векторами называют сложение, вычитание и умножение вектора на число.
Сложение векторов
Определение. Суммой двух векторов 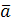 и и 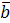 называется вектор называется вектор 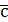 , начало которого совпадает с началом вектора , начало которого совпадает с началом вектора 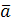 , а конец – с концом вектора , а конец – с концом вектора 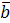 , отложенного из конца вектора , отложенного из конца вектора 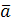 (правило треугольника).
Суммой векторов (правило треугольника).
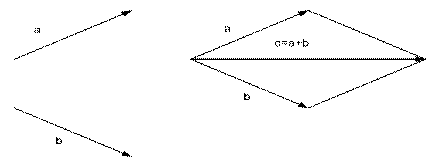
Суммой векторов 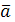 и и 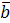 называется такой третий вектор называется такой третий вектор 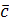 , что при совмещенных началах этих трех векторов, векторы , что при совмещенных началах этих трех векторов, векторы 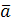 и и 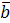 служат сторонами параллелограмма, а вектор служат сторонами параллелограмма, а вектор 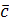 – его диагональю (называется сложением по правилу параллелограмма). – его диагональю (называется сложением по правилу параллелограмма).
| 
|
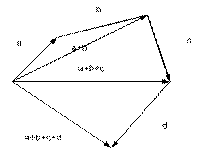
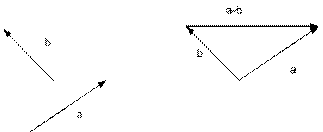
| Из рисунков видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы. Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего. |
Свойства операции сложения векторов:
1. 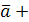 (
( 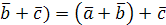 – сочетательное свойство.
– сочетательное свойство.
2. 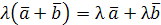 , где
, где 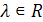 – распределительное свойство относительно суммы векторов.
– распределительное свойство относительно суммы векторов.
3. 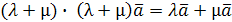 , где
, где 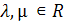 – распределительное свойство относительно суммы чисел.
– распределительное свойство относительно суммы чисел.
Если векторы заданы их разложениями по базисным ортам 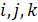 , то при сложении векторов складываются их соответствующие координаты.
, то при сложении векторов складываются их соответствующие координаты.
Пусть 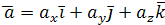 и
и 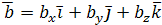 ,
,
тогда 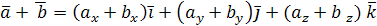 .
.
Рассмотрим это на примере декартовой системы координат:
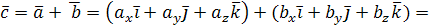
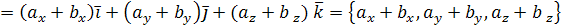
Вычитание векторов
Определение. Разностью векторов 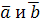 называют вектор называют вектор 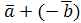 . Второе слагаемое является вектором, противоположным вектору . Второе слагаемое является вектором, противоположным вектору 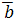 по направлению, но равным ему по длине.
Таким образом, операция вычитания векторов заменяется на операцию сложения по направлению, но равным ему по длине.
Таким образом, операция вычитания векторов заменяется на операцию сложения 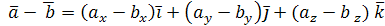 .
Произведение вектора на скаляр
Определение. Произведением вектора .
Произведение вектора на скаляр
Определение. Произведением вектора 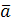 на скаляр на скаляр 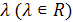 называется вектор называется вектор 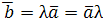 , который удовлетворяет условиям: , который удовлетворяет условиям:
| 
|
1) 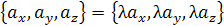 ;
;
2) 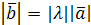 ;
;
3) 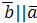 ;
;
4) 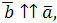 если
если 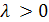 ;
; 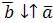 , если
, если 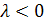 .
.
Следовательно, если векторы 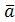 и
и 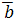 коллинеарные, то
коллинеарные, то 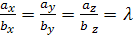 .
.
| <== previous lecture | | | next lecture ==> |
| Свойства обратной матрицы | | | Базис на прямой, на прямой, на плоскости, в пространстве. |