Определение линейного пространства.

Date: 2015-10-07; view: 322.

Расстояние от точки до прямой: на плоскости.

Теорема.Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

.

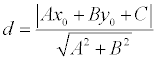Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов x и y из L отвечает элемент x + yиз L, называемый суммой x и y, причём:

x + y = y + x− сложение коммутативно;

x + (y + z) = (x + y) + z− сложение ассоциативно;

x +0= x − существует единственный нулевой элемент 0( x +0= x для любого x из L);

x + (− x)= 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0для любого x из L).

2. Каждой паре x и α, где α −число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:

α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;

1·x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.