Размерность линейного пространства. Базис в n-мерном линейном пространстве. Теорема о разложении вектора в линейном пространстве по базису.

Date: 2015-10-07; view: 394.

Примеры линейных пространств.

1. Множество векторов на плоскости и множество векто-

ров в пространстве образуют линейные пространства (предло-

жение 4.1).

2. Множество матриц Mm´n фиксированного размера образУ

ют линейное пространство (п. 1.3).

3. Нулевой элемент q сам по себе образует линейное про-

странство, так как, очевидно, выполнены все восемь аксиом ли-

нейного пространства.

4. Координатное пространство Rn . Пусть элементами L

являются упорядоченные наборы действительных чисел, по n

чисел в каждом наборе.

5. Пространство непрерывных на отрезке [a,b] функций.

Пусть L - множество всех функций непрерывных на отрезке [a,b]

и tÎ[a,b].

6. Пространство многочленов степени меньше n.

7. Множество решений однородной (приведённой) системы

линейных уравнений образует линейное пространство.

Если в линейном пространстве 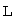существует линейно независимая система из 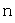векторов, а любая система из 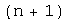-го вектора линейно зависима, то число 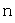называется размерностью пространства 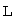и обозначается 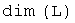. В этом случае пространство 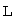называют 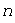-мерным линейным пространством или 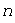-мерным векторным пространством

Любая упорядоченная линейно независимая система 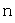векторов 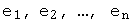линейного пространства 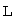образует базис пространства и любой вектор 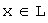единственным образом выражается через векторы базиса: .

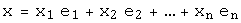Разложением вектора а по базису (e1,e2,e3) называется его запись в виде
a=a1*e1+a2*e2+a3*e3
жирным выделил вектора. Ну или записав в укороченном виде

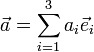
коэффициенты a1,a2,a3 - коэффициенты разложения вектора a в базисе e1,e2,e3
Для декартовой системы координат базисными векторами являются единичные вектора i, j, k, а коэффцициенты разложения называются компонентами вектора a