
Определение Евклидова пространства.
Date: 2015-10-07; view: 371.
Линейное пространство 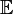 называется евклидовым, если в этом пространстве определена операция, ставящая в соответствие паре векторов
называется евклидовым, если в этом пространстве определена операция, ставящая в соответствие паре векторов 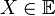 и
и 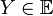 вещественное число, называемое скалярным произведением векторов
вещественное число, называемое скалярным произведением векторов 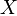 и
и 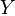 , и обозначаемое
, и обозначаемое 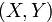 ; при этом операция подчиняется аксиомам:
; при этом операция подчиняется аксиомам:
1. 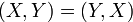 для
для 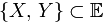 ;
;
2. 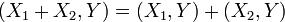 для
для 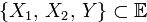 ;
;
3. 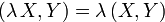 для
для 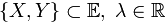 ;
;
4. 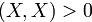 для
для 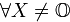 ,
, 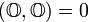
32) Неравенство Коши́ — Буняко́вского
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца («неравенство КБШ»), хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
| <== previous lecture | | | next lecture ==> |
| Размерность линейного пространства. Базис в n-мерном линейном пространстве. Теорема о разложении вектора в линейном пространстве по базису. | | | Формулировка |