Формулировка

Date: 2015-10-07; view: 379.

Пусть дано линейное пространство L со скалярным произведением 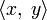. Пусть 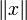— норма, порождённая скалярным произведением, то есть 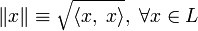. Тогда для любых 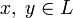имеем:

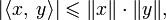
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).