
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ ВЫСКАЗЫВАНИЯМИ
СВОДНАЯ ТАБЛИЦА ВОЗМОЖНЫХ СВЯЗЕЙ МЕЖДУ ВЫСКАЗЫВАНИЯМИ
В логике принято характеризовать логические союзы таким способом, при котором логическое значение сложного высказывания ставится в зависимость от логических значений входящих в его состав простых. Приведем таблицу соответствующих языковых эквивалентов логических связей.
| Варианты значений | Выражения логической связи через известные союзы | Возможные соответствия в естественном языке | ||||
| p | и | и | л | л | ||
| q | и | л | и | л | ||
| p R1 q | и | и | и | и | p v ¬ p ^ q v ¬ q | Закон исключенного третьего |
| p R2 q | и | и | и | л | p v q | Слабая дизъюнкция |
| p R3 q | и | и | л | и | 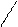  p q p q
| Репликация ( обратная импликация) |
| p R4 q | и | л | и | и | 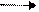 p q p q
| Импликация |
| p R5 q | л | и | и | и | ¬ p v ¬ q | Или не-p, или не-q |
| p R6 q | и | и | л | л | (q v ¬ q) ^ p | Независимо от того, q или не-q , но p |
| p R7 q | и | л | л | и | p ↔ q | Эквиваленция |
| p R8 q | л | л | и | и | (q v ¬ q) ^ ¬ p | Независимо от того, q или не-q , но не -p |
| p R9 q | л | и | и | л |   p V q p V q
| Строгая дизъюнкция |
| p R10 q | и | л | и | л | (p v ¬ p) ^ q | Независимо от того, p или не-p , но q |
| p R11 q | л | и | л | и | (p v ¬ p) ^ ¬ q | Независимо от того, p или не-p , но не -q |
| p R12 q | и | л | л | л | p ^ q | Конъюнкция |
| p R13 q | л | и | л | л | p ^ ¬ q | Хотя и p, но не-q |
| p R14 q | л | л | и | л | ¬ p ^ q | Хотя и не- p, но q |
| p R15 q | л | л | л | и | ¬ p ^ ¬ q | Ни p, ни q |
| p R16 q | л | л | л | л | ( p ^ ¬ p) v ( q ^ ¬ q ) | Логическое противоречие |
Сложные высказывания, в составе которых содержится хотя бы одно общее для них простое, могут находиться между собой в определенных отношениях:совместимых, если хотя бы в одном варианте логических значений входящие в их состав простые высказывания окажутся одновременно истинными, илинесовместимых, если ни в одном варианте логических значений одновременно истинными быть не могут.
Совместимые высказывания могут находиться в следующих отношениях:
а) полной совместимости, или равнозначности;
б) частичной совместимости;
в) следования, или подчинения;
г) сцепления.
Несовместимые высказывания могут находиться в отношениях:
а) противоположности;
б) противоречия.
Кратко охарактеризуем эти отношения.
В отношении равнозначностинаходятся формы сложных высказываний, имеющих одинаковые логические значения по всем строчкам своих таблиц, т.е. когда истинному значению одного высказывания соответствует истинное значение другого, а ложному значению одного — ложное значение другого. В этом отношении находятся, к примеру, высказывания форм и p → q и ¬ q → ¬p
«Если комнатные цветы не поливать, то они засохнут» и «Если цветы не засохли, то их поливали». Формулы, выражающие равнозначные высказывания, называются логически эквивалентными.
| P | Q | P → Q | ¬Q → ¬P |
| И | И | И | И |
| И | Л | Л | Л |
| Л | И | И | И |
| Л | Л | И | И |
В отношении частичной совместимости находятся высказывания, которые могут быть одновременно истинными, но не одновременно ложными: «Если повысить производительность труда, то произойдет снижение себестоимости продукции» и «Если снизится себестоимость продукции, то произойдет повышение производительности труда». Им соответствуют формы p → q и q → p
| P | Q | P → Q | Q → P |
| И | И | И | И |
| И | Л | Л | И |
| Л | И | И | Л |
| Л | Л | И | И |
В отношении следования, или подчинения, находятся высказывания, истинному значению одного из которых соответствует истинное значение другого, но не наоборот — например, высказывания «Если у четырехугольника попарно параллельные стороны, то этот четырехугольник — параллелограмм, а если четырехугольник — параллелограмм, то его диагонали, пересекаясь, делятся пополам» и «Если у четырехугольника попарно параллельные стороны, то его диагонали, пересекаясь, делятся пополам», которым соответствуют формы
(p → q) ^ ( q → r) и p ↔ r
| p | q | r | (p → q) ^ (q → r) | p ↔ r |
| и | и | и | и | и |
| и | и | л | л | л |
| и | л | л | л | и |
| л | и | и | и | и |
| и | л | л | л | л |
| л | и | л | л | и |
| л | л | и | и | и |
| л | л | л | и | и |
В отношении сцепления находятся высказывания, истинность (ложность) одного из которых не исключает ложности (истинности) другого высказывания «Если утром упадет туман, то днем будет солнечная погода» и « Если утром не упадет туман, то днем все равно будет солнечная погода», имеющие формы p → q и ¬p → q
| p | q | p → q | ¬p → q |
| И | И | И | И |
| И | Л | Л | И |
| Л | И | И | И |
| Л | Л | И | Л |
В отношении противоположности находятся высказывания, которые не могут быть одновременно истинными, но могут быть одновременно ложными. Например, высказывания «Загорелся красный свет светофора и водитель остановился» и «Загорелся красный свет светофора и водитель не остановился», имеющие формы
p ^ q и p ^ ¬ q
| p | q | p ^ q | p ^ ¬q |
| И | И | И | Л |
| И | Л | Л | И |
| Л | И | Л | Л |
| Л | Л | Л | Л |
В отношении противоречия находятся высказывания, которые не могут быть одновременно истинными и ложными - «Если идет дождь, то небо покрыто тучами» и «Хотя и идет дождь, но небо не покрыто тучами», имеющие формы p → qи p ^ ¬q
| p | q | p → q | p ^ ¬q |
| И | И | И | Л |
| И | Л | Л | И |
| Л | И | И | Л |
| Л | Л | И | Л |
| <== предыдущая страница | | | следующая страница ==> |
| УСЛОВНЫЕ (ИМПЛИКАТИВНЫЕ) ВЫСКАЗЫВАНИЯ | | | ОТРИЦАНИЕ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ |
Дата добавления: 2014-02-26; просмотров: 628; Нарушение авторских прав

Мы поможем в написании ваших работ!