
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Интегралы вида где и - целые числа
Таблица интегралов
1) 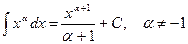 .
.
2) 
3) 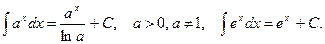
4) 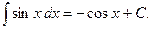
5) 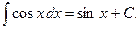
6) 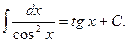
7) 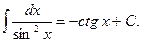
8) 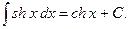
9) 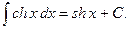
10) 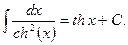
11) 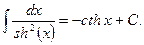
12) 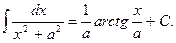
13) 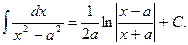
14) 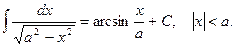
15) 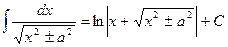
(если под корнем 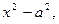 то
то 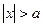 ).
).
1.4 Формула замены переменной. Пусть функции 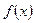 и
и 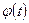 определены соответственно на промежутках Т и Т1 , причем
определены соответственно на промежутках Т и Т1 , причем 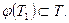 Если функция f имеет на Т первообразную F(x) и, следовательно,
Если функция f имеет на Т первообразную F(x) и, следовательно,
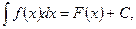
а функция 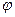 дифференцируема на Т1, то функция
дифференцируема на Т1, то функция 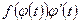 имеет на Т1 первообразную
имеет на Т1 первообразную 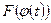 и
и
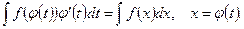 (1)
(1)
Иначе говоря, сделаем сначала подстановку 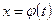 , а затем возьмем интеграл, или сначала возьмем интеграл, а потом сделаем указанную подстановку, - результат будет один и тот же.
, а затем возьмем интеграл, или сначала возьмем интеграл, а потом сделаем указанную подстановку, - результат будет один и тот же.
Отметим, что формулу (1) бывает целесообразно использовать и в обратном порядке, т.е. справа налево. Именно, иногда удобно вычисление интеграла 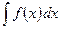 с помощью соответствующей замены переменного
с помощью соответствующей замены переменного 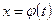 свести к вычислению интеграла
свести к вычислению интеграла
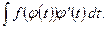
В случае, когда функция 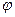 имеет обратную
имеет обратную 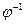 , то воспользовавшись формулой (1) справа налево, сводим вычисление
, то воспользовавшись формулой (1) справа налево, сводим вычисление 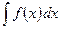 к вычислению
к вычислению 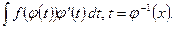 Эта формула называется обычно формулой интегрирования заменой переменного.
Эта формула называется обычно формулой интегрирования заменой переменного.
1.5 Формула интегрирования по частям. Если функции u(x), v(x) дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл 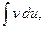 то на нем существует и интеграл
то на нем существует и интеграл 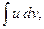 причем
причем
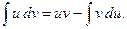
Эта формула называется формулой интегрирования по частям. Дадим некоторые рекомендации для использования этой формулы. А именно, что целесообразно обозначить под интегралом через функцию u, а что брать в качестве дифференциала dv. Пусть Р(х) – некоторый многочлен. Тогда
1) 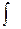
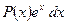
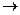
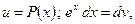
2) 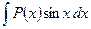
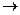
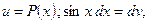
3) 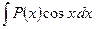
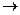
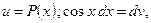
4) 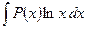
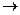
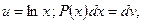
5) 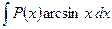
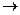
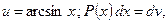
6) 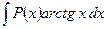
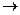
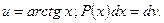
Отметим, что при необходимости формулу интегрирования по частям можно применять несколько раз подряд.
1.6 Интегрирование рациональных дробей. Рассмотрим интеграл 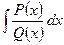 от рациональной функции. Метод нахождения таких интегралов основан на возможности разложения любой правильной рациональной дроби на сумму элементарных дробей. К элементарным относятся дроби вида
от рациональной функции. Метод нахождения таких интегралов основан на возможности разложения любой правильной рациональной дроби на сумму элементарных дробей. К элементарным относятся дроби вида
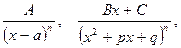
где n – некоторое натуральное число, а трехчлен 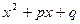 не имеет действительных корней.
не имеет действительных корней.
Остановимся подробнее на этапах этого метода.
1) Если дробь  неправильная, то поделив числитель на знаменатель, выделим целую часть
неправильная, то поделив числитель на знаменатель, выделим целую часть
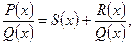
при этом степень многочлена 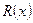 меньше степени многочлена
меньше степени многочлена 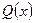 .
.
2) Разложим знаменатель 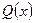 на множители
на множители 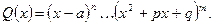
3) Представим правильную дробь 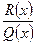 в виде суммы элементарных дробей
в виде суммы элементарных дробей
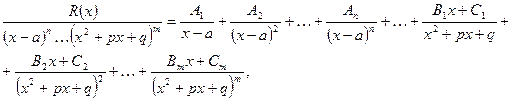
где коэффициенты 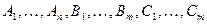 пока не определены.
пока не определены.
4) Находим в последнем разложении неизвестные коэффициенты и сводим тем самым интеграл 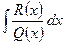 к вычислению суммы интегралов от элементарных дробей.
к вычислению суммы интегралов от элементарных дробей.
1.7 Интегралы вида 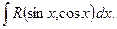
а) В общем случае интегралы вида 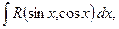 где
где 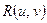 - рациональная функция двух переменных, сводятся к интегралу от рациональной функции одной переменной путем универсальной тригонометрической подставки
- рациональная функция двух переменных, сводятся к интегралу от рациональной функции одной переменной путем универсальной тригонометрической подставки 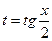 ,
, 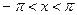 . Действительно,
. Действительно,
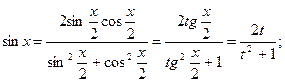
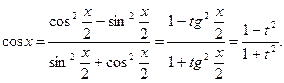
Из равенства 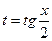 следует, что
следует, что 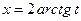 и
и 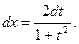
Тогда
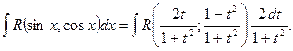
б) Если подынтегральная функция имеет вид 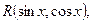 но
но 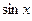 и
и 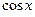 входят только в четных степенях (допускается наличие произведения
входят только в четных степенях (допускается наличие произведения 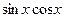 ), то удобно применять подстановку
), то удобно применять подстановку 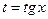 или
или 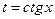 .
.
В этом случае
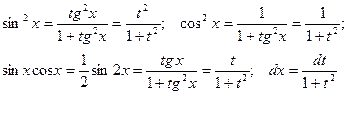 .
.
в) Интегралы 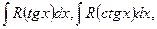 где
где 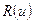 - рациональная функция, сводятся к интегралу от рациональной функции переменной
- рациональная функция, сводятся к интегралу от рациональной функции переменной 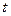 заменой
заменой 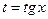 или
или 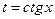 :
:
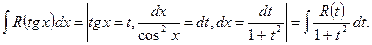
а) Пусть хотя бы одно из целых чисел 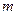 или
или 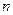 - нечетное, например,
- нечетное, например, 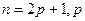 - некоторое целое число. Тогда
- некоторое целое число. Тогда
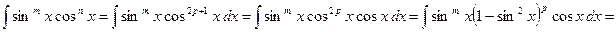
=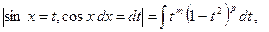
и исходный интеграл сводится к интегралу от рациональной функции.
б) Пусть 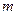 и
и 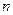 - четные неотрицательные целые числа. Тогда интеграл
- четные неотрицательные целые числа. Тогда интеграл 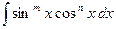 вычисляют с использованием тригонометрических формул понижения степени:
вычисляют с использованием тригонометрических формул понижения степени:
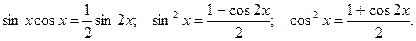
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства неопределенного интеграла | | | Интегрирование некоторых иррациональных выражений |
Дата добавления: 2014-02-28; просмотров: 749; Нарушение авторских прав

Мы поможем в написании ваших работ!