
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Интегрирование некоторых иррациональных выражений
Интегралы вида
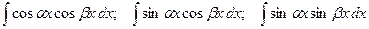
вычисляются при помощи формул:

а) Рассмотрим интегралы вида
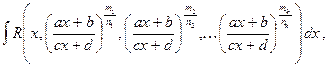 (2)
(2)
где R – рациональная функция от  переменных,
переменных, 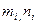 - натуральные числа,
- натуральные числа, 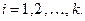
Пусть S – наименьший общий знаменатель дробей 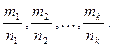 Тогда с помощью замены
Тогда с помощью замены 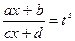 интеграл (2) сводится к интегралу от рациональной функции переменного
интеграл (2) сводится к интегралу от рациональной функции переменного 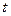 .
.
Рассмотрим, например, интеграл
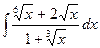 .
.
Выбирая наименьший общий знаменатель дробей  (то есть 6), сделаем замену
(то есть 6), сделаем замену 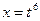 . Тогда
. Тогда 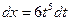 и
и
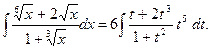
Остается вычислить последний интеграл, как это указано в 1.6.
б) При вычислении интегралов вида
1)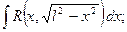 2)
2) 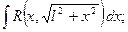 3)
3) 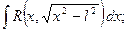
где 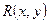 - рациональная функция, удобно пользоваться следующими тригонометрическими подстановками соответственно:
- рациональная функция, удобно пользоваться следующими тригонометрическими подстановками соответственно:
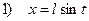 или
или 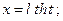 2)
2) 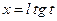 или
или 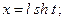 3)
3) 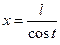 или
или 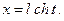
В этом случае исходные интегралы сводятся к интегралам, описанным в 1.7 и в 1.8.
в) Интегралы от дифференциального бинома, т.е. интегралы вида
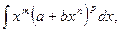
где 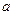 и
и 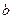 - действительные числа, а
- действительные числа, а 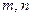 и
и 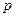 - рациональные, сводятся к интегралу от обычной рациональной функции одного переменного только в трех случаях (теорема Чебышева):
- рациональные, сводятся к интегралу от обычной рациональной функции одного переменного только в трех случаях (теорема Чебышева):
1) 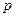 -целое число; 2)
-целое число; 2) 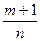 - целое число; 3)
- целое число; 3)  - целое число.
- целое число.
В первом случае это делается при помощи подстановки 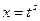 , где s – общий знаменатель дробей
, где s – общий знаменатель дробей 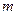 и
и 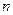 ; во втором случае можно положить
; во втором случае можно положить 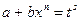 , где s – знаменатель дроби
, где s – знаменатель дроби 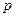 ; в третьем применяют подстановку
; в третьем применяют подстановку 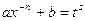 , где s – знаменатель дроби
, где s – знаменатель дроби 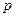 .
.
1.11 Определенный интеграл. Понятие определенного интеграла Римана и его свойства хорошо изложены в литературе (см. /1 – 4/), поэтому мы останавливаться на этом не будем. Рассмотрим лишь способы вычисления определенных интегралов и их приложения.
а) Формула Ньютона-Лейбница (основная теорема интегрального исчисления).
Пусть функция 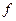 непрерывна на отрезке
непрерывна на отрезке 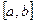 . Если функция
. Если функция 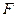 является произвольной ее первообразной на этом отрезке, то
является произвольной ее первообразной на этом отрезке, то
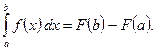
б) Формула замены переменной.
Пусть
1) функция 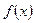 непрерывна на отрезке
непрерывна на отрезке 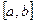 ;
;
2) функция 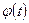 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 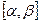 , причем
, причем 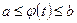 для всех
для всех 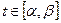 , и
, и 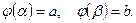
Тогда
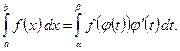
Таким образом, при замене переменного 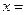
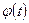 в определенном интеграле
в определенном интеграле 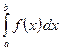 следует всюду формально заменить
следует всюду формально заменить  на
на 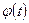 и соответственно изменить пределы интегрирования.
и соответственно изменить пределы интегрирования.
в) Формула интегрирования по частям.
Если функции 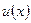 и
и 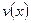 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке 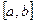 , то
, то

| <== предыдущая страница | | | следующая страница ==> |
| Интегралы вида где и - целые числа | | | Вычисление площадей |
Дата добавления: 2014-02-28; просмотров: 807; Нарушение авторских прав

Мы поможем в написании ваших работ!