Кинематика твердого тела

Задача 2

Задача 1

Здесь рычаг манипулятора поворачивается в горизонтальной плоскости и одновременно вдоль рычага перемещается ползун с захватом (материальная точка А) (рис. 5).

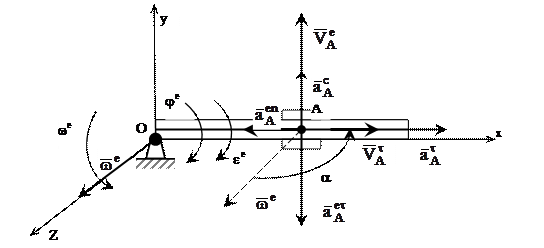
Рис. 5

Дано: 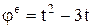(рад.), 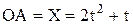(м).

Найти: 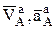при t=1 c.

Решение: Движение точки А является сложным: относительное движение вдоль рычага и переносное, т.е. поворот вместе с рычагом.

Сначала определим положение точки А в её относительном движении при

t=1 c и найдем в этом положении 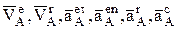по величине и направлению.

Для относительного движения

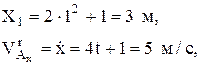
т.к. движение по прямой вдоль оси Х, то 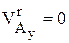и 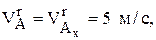аналогично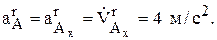

Для переносного движения:

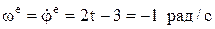– угловая скорость переносного движения;

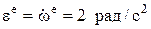– его угловое ускорение (знак « - » у w^e , полученный после дифференцирования и подстановки значения t означает, что направление вращения против положительного отсчета координаты j, принятого в задаче, а знак « + » у e^e означает, что направление ускорения совпадает с j);

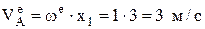– вращательная скорость перпендикулярна радиусу ОА и направлена в сторону w^e;

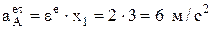– перпендикулярна радиусу в сторону e^e;

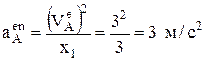– по радиусу к центру О.

.

Итак 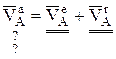, т.к. 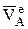перпендикулярно 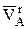, то последнее уравнение можно не проецировать на оси Х и Y, а использовать теорему Пифагора

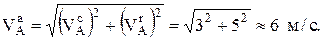
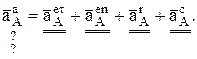
После проецирования на оси Х и Y получим

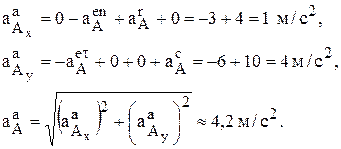
Рассмотрим случай, когда абсолютные кинематические характеристики движения рассматриваемой точки легко находятся, а с помощью уравнений (5) определяются характеристики переносного и относительного движения в определенном заданном положении механизма (рис. 6).

Дано: V₁ =0,2 м/с, а₁ =0,1 м/с², j=60°, Н=0,5 м.

Найти: w₃, e₃.

Решение: Механизм состоит из трех звеньев: звено 1 – шток гидроцилиндра (ведущее); звено 2 – ползун (промежуточное), которое скользит вдоль звена 3 – кулиса (ведомое). Тем самым поступательное движение звена 1 преобразовывается в поворотное звена 3.

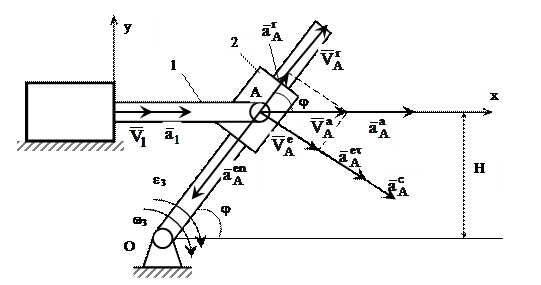
Рис. 6

При решении применяется распространенный прием кинематики: переход от одного звена к другому через их общую точку (здесь точка А). При этом учитывается, что кинематические характеристики этой точки одинаковы, но они определяются сначала по формулам и правилам движения первого звена, а затем второго соединенного с ним.

В данном случае звено 1 совершает поступательное движение по прямой (подробнее такое движение рассмотрено ниже), а значит характеристики движения всех точек в данный момент одинаковы, т.е. 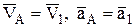. При этом для точки А звена 1 это характеристики относительно неподвижной системы отсчета, т.е. абсолютные. Для этой же точки звена 2 (его можно принять материальной точкой) уже можно говорить о сложном движении, т.к. точка А скользит вдоль кулисы 3 (относительное движение) и поворачивается вместе с ней вокруг центра О (переносное). Таким образом, легко разложить найденные выше характеристики абсолютного движения на характеристики переносного и относительного движения точки А звена 2 (рис. 6).

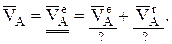
Учитывая, что 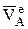перпендикулярен 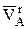, последнее уравнение можно не проецировать на оси Х и Y, а сразу записать

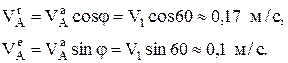
Если 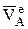вращательная скорость точки А звена 2 и звена 3 с радиусом вращения ОА, то угловую скорость звена 3 можно найти так

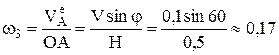рад/с.

Аналогично рассуждая можно для ускорений получить с учетом (5) следующее

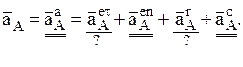
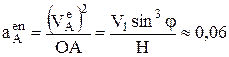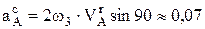Здесь м/с²

м/с².

Спроецировав последнее векторное уравнение на оси Х и Y с учетом направлений векторов, показанных на рис. 6 получим

.

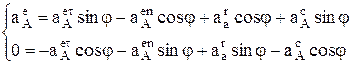Можно обратить внимание, что взаимно перпендикулярные вектора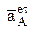и 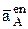позволяют находить проекцию на одну ось через синус, а на другую ось через косинус одного угла j. То же справедливо и для одного какого-то вектора при его проецировании на ось Х, а затем ось Y .

Решая последнюю систему относительно двух неизвестных 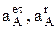, т.е. модулей соответствующих векторов легко можно найти их значения. Если в результате расчетов значение окажется со знаком « - », то соответствующий вектор направлен противоположно направлению первоначально принятому на рис. 6 (вектора 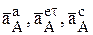могут быть определены по направлению точно, по ранее рассмотренным правилам).

Угловое ускорение звена e₃ совпадает с направлением вектора 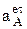, а величина его находится с учетом радиуса вращения точки А звеньев 2 и 3, т.е.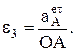

В данном разделе будут рассмотрены только три наиболее часто встречающихся в механизмах движения его звеньев (твердых тел).

Дата добавления: 2014-02-26; просмотров: 561; Нарушение авторских прав

Мы поможем в написании ваших работ!