Рассеяние в трансформаторах с концентрическими и чередующимися обмотками

Короткое замыкание трехфазных трансформаторов

Здесь мы имеем в виду только случай трехфазного, или так называемого симметричного, короткого замыкания, когда замкнуты накоротко все три фазы трансформатора.

Некоторые специальные случаи короткого замыкания — однофазного и двухфазного – рассматриваются ниже.

В противоположность холостому ходу симметричное короткое замыкание трехфазных трансформаторов не имеет особых специфических особенностей по сравнению с коротким замыканием однофазного трансформатора. Это объясняется тем, что при коротком замыкании, в противоположность холостому ходу, сталь не насыщена в соответствии с чем токи и мощности распределяются между фазами симметрично и формы кривых ЭДС не нарушаются.

На этом основании мы можем распространить на случай трехфазного короткого замыкания все, что было сказано выше относительно короткого замыкания однофазного трансформатора. Следует только помнить, что, производя расчеты, мы должны вести их на одну фазу.

Если МДСдвух обмоток трансформатора находятся в строгом равновесии между собой, т. е. 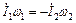, то полный ток 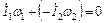. В этом случае нет потока результирующей МДС, сцепленного с обеими обмотками, а есть только потоки, называемые потоками рассеяния, сцепленные каждый со своей обмоткой. К этим условиям очень близко подходит трансформатор в режиме короткого замыкания (см. рис. 6.1). В общем случае 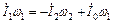[см. формулу (13-15б)] или 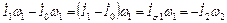т. е. в этом случае потоки рассеяния создаются токами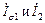

Такое определение рассеяния может быть легко распространено на многообмоточный трансформатор.

Явление рассеяния определяет ряд основных свойств трансформатора как в стационарном «режиме его работы, влияя на изменение вторичного напряжения, условия параллельной работы, добавочные потери в трансформаторе и т.д., так и в режиме внезапного короткого замыкания, определяя величину токов короткого замыкания и связанные с ними эффекты механического и термического характера. Поэтому возможно точное определение индуктивности и ЭДС рассеяния или соответственно величины напряжения короткого замыкания является одним из основных вопросов теории трансформатора.

Для расчета индуктивности и ЭДС рассеяния трансформатора необходимо знать пространственное распределение потоков рассеяния в нем. Оно очень сложно даже для сравнительно простых обмоток и зависит от их взаимного расположения и их относительных размеров. Поэтому пользуются методом приведения, состоящим, как мы уже говорили, в том, что действительную сложную картину поля рассеяния заменяют расчетной, которая отличается большей простотой, но дает те же количественные результаты, что и действительная картина.

Расчет индуктивности рассеяния концентрических обмоток. Рассмотрим сначала простейший случай, когда первичная и вторичная обмотки представляют собой цилиндры одинаковой высоты с одинаковым распределением МДС по высоте обмотки, причем 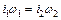. На рис. 6.7, а показана действительная картина поля рассеяния для двух концентрических обмоток с большим отношением размеров в осевом и радиальном направлениях (высоты обмотки к ее ширине). По методу Роговского такую картину заменяют картиной, показанной на рис. 6.7, б.

Здесь прежде всего следует обратить внимание на расположение центров О₁ и О₂ первичного и вторичного потоков рассеяния. Если бы каждая из обмоток существовала отдельно от другой и была окружена однородной средой, то центр потока такой обмотки находился бы на пересечении диагоналей изображающего ее прямоугольника. Но в нашем случае вследствие бокового распора трубок центры потоков рассеяния смещаются в противоположные стороны на края обмоток, продолжая оставаться на средней высоте последних. При этом предполагается, что все трубки потока рассеяния идут параллельно образующим цилиндров и имеют расчетную длину 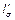Эта длина вводится в расчет магнитного сопротивления трубки, тогда как сопротивление остальной части трубки принимается равным нулю. Согласно теоретическим исследованиям, можно приближенно считать, что

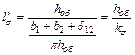(6.15)

Здесь 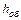— высота обмотки; — ширина первичной и вторичной обмоток; 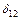— ширина зазора между обмотками, 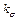— коэффициент приведения высоты обмотки к расчетной длине линий поля рассеяния.

Так как ширина обмоток и зазор обычно невелики по сравнению с 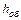, то для обычных концентрических обмоток коэффициент .

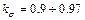Для потока рассеяния, изображенного на рис. 6.7, б, можно построить кривую МДС В центрах О₁ и О₂ МДС равны нулю; затем МДС растут пропорционально расстояниям, на которых находятся трубки первичного и вторичного потоков рассеяния от центра О₁ или соответственно О₂. В зазоре 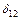, между обмотками МДС не изменяется, причем одну половину зазора мы условно считаем заполненной линиями первичного рассеяния, а другую — вторичного.

Рис. 6.7. Поле рассеяния трансформатора с концентрической обмоткой: а—действительная картина поля; 6 — приведенная

Рассчитаем индуктивность рассеяния какой-нибудь одной обмотки, например обмотки 2, предполагая, что по числу витков она приведена к обмотке 1. Расчет состоит из расчета индуктивности 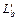по ширине обмотки 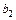, где МДС непрерывно изменяется, и из расчета индуктивности 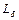по ширине 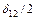, где МДС остается постоянной. Искомая индуктивность 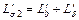. Ход расчета носит типичный характер и ведется в следующем порядке: а) выделяем элементарную трубку и определяем ее МДС и поток при протекании по обмотке тока в 1 а, б) определяем число потокосцеплений данной элементарной трубки и в) рассчитываем число потокосцеплений всех элементарных трубок, находящихся в заданных пределах.

Для расчета индуктивности выделим элементарную трубку на расстоянии х от внутренней образующей вторичной обмотки. При 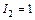а МДС этой трубки будет

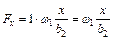
Магнитное сопротивление той же трубки

,

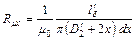где 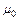— магнитная проницаемость воздуха (масла) и 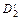— внутренний диаметр вторичной обмотки.

Следовательно, поток dФ_x выделенной нами элементарной трубки и число ее потокосцеплений 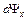будут равны:

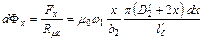
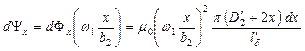
Число потокосцеплений по ширине обмотки 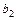при токе 1 а, т.е. индуктивность обмотки, будет

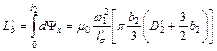
Второе слагаемое, соответствующее ширине зазора 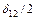, определяется аналогично первому с той только разницей, что трубка, находящаяся в зазоре, создается всей МДС вторичной обмотки и сцепляется со всеми витками последней. Поэтому число потокосцеплений по ширине 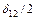будет

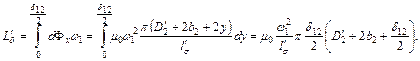
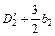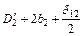С достаточным приближением можно считать, что суммы , и представляют собой каждая средний диаметр 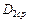вторичной обмотки. Тогда индуктивность вторичной обмотки будет

.

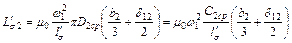где 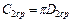— средняя длина витка вторичной обмотки. Если проделать те же расчеты для первичной обмотки, то получим:

.

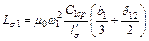где 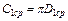— средняя длина витка первичной обмотки. Следовательно, индуктивность рассеяния обеих обмоток будет

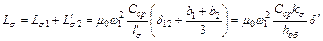(6.16)

Здесь 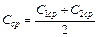представляет собой среднюю длину витка обеих обмоток, а 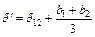— так называемую приведенную ширину зазора между обмотками.

Так как 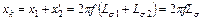; то индуктивное сопротивление трансформатора

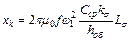(6.17)

Соответственно индуктивная составляющая напряжения короткого замыкания [см. формулу (6.8б)]:

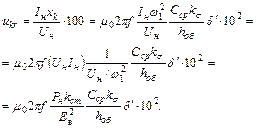(6.18)

Здесь – номинальная мощность трансформатора, выраженная в В∙А; Е_в – ЭДС на виток; k_ст – коэффициент, показывающий, какая часть номинальной мощности приходится на один стержень: в однофазных трансформаторах, в которых обмотка располагается обычно на двух стержнях, k_ст = 1/2, в трехфазных трансформаторах, где фазная обмотка расположена обычно на каком – нибудь одном стержне, k_ст = 1/3.

Обычно мощность Р_н „ выражают в кВ∙А и размеры – в см. Так как, кроме тог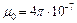о, , то

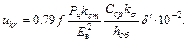(6.19)

Формула (6.19) имеет весьма важное значение, так как она связывает с величиной 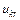, ряд величин, определяющих в основном конструкцию трансформатора.

Расчет индуктивности рассеяния чередующихся обмоток. Все изложенное выше о расчете 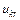концентрических обмоток может быть с соответствующими изменениями применено и для расчета 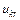, обмоток чередующихся.

В схематическом виде чередующаяся обмотка показана на рис. 6.8, а. Обмотки ВН и НН состоят нз одинакового числа катушек, но одна нз катушек обмотки НН разделена на две полукатушки, расположенные в верхней и нижней частях обмотки. Центры, вокруг которых образуются линии потока рассеяния, показаны жирными точками. Такая действительная картина потрка рассеяния заменена приведенной (рис. 6.8, б), в которой все линии потока, показанные штриховыми линиями, идут перпендикулярно оси стержня (сравнить с картиной потока на рис. 6.7, б) и имеют расчетную длину 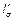. Кривая распределения МДС рассматриваемой обмотки дана на рис. 6.8, в. Так как кривая МДС располагается симметрично относительно оси ординат, то чередующаяся обмотка на рис. 6.8, а называется симметричной. Мы видим, что всю обмотку можно разделить на п последовательно соединенных групп, состоящих каждая из двух по- лукатушек обмоток ВН и НН. Кривая МДС каждой группы повторяет собой кривую МДС концентрической обмотки на рис. 6.7, б. Поэтому при определении индуктивности чередующейся обмотки можно исходить из тех же формул (6.16) и (6.17), которые были выведены для концентрической обмотки, при условии, что чередующуюся обмотку мы рассматриваем как обмотку, состоящую из п последовательно соединенных групп с числом витков 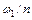в каждой. В этом случае соответственно формуле (6.18) имеем:

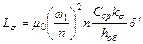(6.20)

Следовательно,

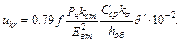(6.21)

Для чередующихся обмоток коэффициент 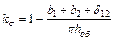обычно находится в пределах 0,65 — 0,80.

Дата добавления: 2014-03-11; просмотров: 661; Нарушение авторских прав

Мы поможем в написании ваших работ!