Диффузионный пограничный слой

Аналогично понятиям о гидромеханическом и тепловом пограничных слоях при изучении массообмена можно говорить А об образовании специфического пограничного слоя. В пределах этого слоя концентрация 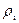и парциальное давление мигрирующего компонента заметно изменяются (от 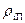и 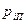на поверхности раздела фаз до 0,99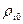и 0,99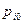на внешней границе слоя). Вне пограничного слоя эти величины не меняются и их градиенты 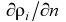и 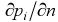равны нулю. Диффузионный пограничный слой образуется, например, при испарении, при сушке материалов, при сублимации, адсорбции и десорбции, конденсации парогазовых смесей и в других случаях.

Рассмотрим для наглядности процесс испарения жидкости при протекании над ее поверхностью ламинарного потока парогазовой смеси с небольшой концентрацией пара (см. рис. 9.1). В этом случае непосредственно у поверхности жидкости образуется очень тонкий слой смеси, содержащий насыщенный пар, парциальное давление которого рiп определяется температурой поверхностного слоя жидкости t . Поскольку концентрация и парциальное давление пара в более вехних слоях значительно меньше, то возникает концентрационная диффузия и "молекулы пара! направляются вглубь потока. С увеличением x диффузия проникает все глубже в поток, толщина слоя растет, а верхняя часть эпюры распределения р становится все более пологой. При некотором 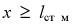в верхней части слоя изменение парциального давления становится настолько малым, что не фиксируется измерительными приборами. Тогда говорят, что при 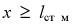слой стабилизировался. Понятно, что вне пограничного слоя массообмен практически не происходит, и для определения потока массы следует анализировать явления в пограничном слое.

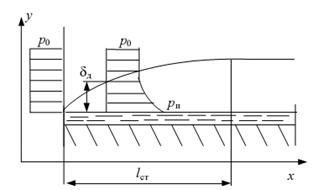
Рис.9.1 Диффузионный пограничный слой.

Дифференциальные уравнения молекулярного массообмена выводятся аналогично рассмотренным ранее дифференциальному уравнению теплопроводности, энергии и другим. Однако теперь, анализируя например уравнение теплового баланса для элементарно малого объема, выделенного внутри пограничного слоя, в рассмотрение необходимо включить все тепловые потоки, в том числе и возникающие в результате массообмена. Конкретно, для определения теплового потока, входящего в элементарный объем по направлению x, в соответствии с формулой (2.73) следует записать

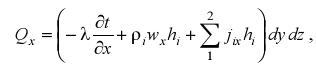
в то время как при выводе дифференциального уравнения теплопроводности использовалось только первое слагаемое.

Оставляя за рамками рассмотрения подробный вывод этих дифференциальных уравнений, приведем лишь их перечень и краткие характеристики:

– дифференциальное уравнение энергии с учетом переноса тепла в результате массобмена, отражающее, как было сказано выше, тепловой баланс при таком процессе;

– дифференциальное уравнение массобмена, отражающее закон сохранения массы для мигрирующего компонента применительно к элементарно малому объему движущейся смеси с протекающей там концентрационной диффузией. Это уравнение имеет вид (в записи через относительную массовую концентрацию)

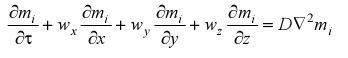(9.3)

и описывает распределение массы i-го компонента внутри пограничного слоя;

– дифференциальное уравнение движения, записанное для смеси в целом;

– дифференциальное уравнение неразрывности для всей смеси.

В такой формулировке эти уравнения составляют замкнутую систему, интегрировать которую можно лишь с учетом условий однозначности.

Отметим еще, что массообменный пограничный слой, как и гидродинамический, может формироваться и при турбулентном течении парогазовой смеси. При этом в ламинарном подслое осуществляется молекулярная диффузия, а в турбулентной части слоя – конвективный массоперенос.

Процессы массобмена, аналогичные рассмотренному принято называть массоотдачей.

Дата добавления: 2014-03-11; просмотров: 594; Нарушение авторских прав

Мы поможем в написании ваших работ!