Косой пространственный изгиб

Рассмотрим изгиб, вызываемый силой, не лежащей в плоскости симметрии.

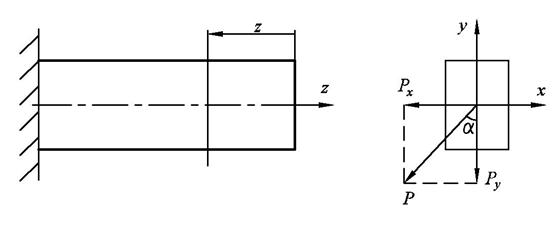
Балка прямоугольного сечения, с защемлённым концом изгибается силой Р, расположенной перпендикулярно продольной оси.

Сечение проводим на расстоянии z от свободной стороны.

Разложим силу Р, принадлежащую сечению, на две составляющие: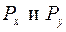

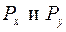- вызывают поперечный изгиб. Косой пространственный изгиб всегда можно свести к двум плоским изгибам.

Изгибающий момент от действия силы 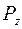будет равен:

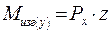
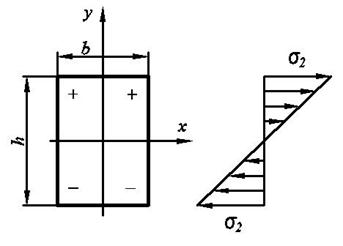
Нормальные напряжения в любой точке, лежащей на расстоянии z от нейтрального слоя, будут равны:

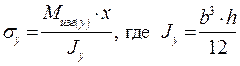
Максимальные нормальные напряжения будут на поверхности при z=b/2 и будут равны:

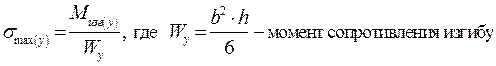
При этом дальние волокна будут растянуты, ближние сжаты.

Изгибающий момент от действия силы 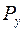будет равен:

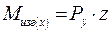
Нормальные напряжения в любой точке, лежащей на расстоянии у от нейтрального слоя, будут равны:

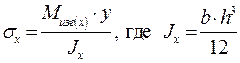
Максимальные нормальные напряжения будут на поверхности при у=h/2 и будут равны:

При этом верхние волокна будут растянуты, нижние сжаты.

Пользуясь законом независимого действия сил определим суммарное максимальное напряжение изгиба, возникающее при одновременном действии моментов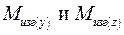

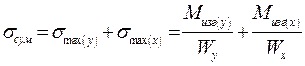
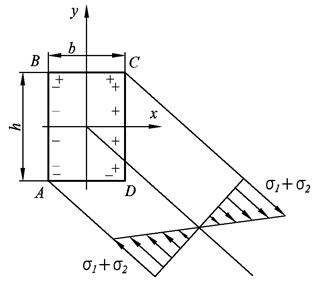
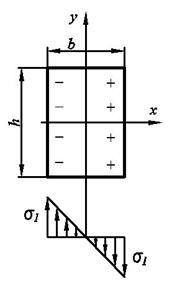
Нейтральная ось проходит через центр тяжести сечения. Точки А и С имеют максимальные значения напряжений. В точке А происходит сжатие, в точке С происходит растяжение.

Дата добавления: 2014-03-13; просмотров: 403; Нарушение авторских прав

Мы поможем в написании ваших работ!