
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Analysis. Summary
Пример
Пусть мы имеем 3 фактора, от которых зависит результатная переменная. Обозначим их через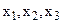 . Значения факторов приведены в таблице.
. Значения факторов приведены в таблице.
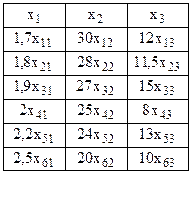
Матрица парных коэффициентов имеет вид:

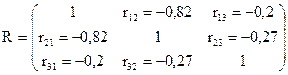 ,
,
т. е. имеет место высокая корреляция между 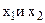 . Кроме того,
. Кроме того,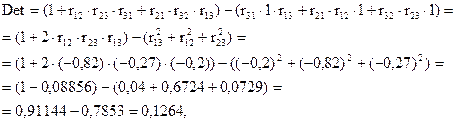 т. е. имеет место значительная мультиколлинеарность факторов.
т. е. имеет место значительная мультиколлинеарность факторов.
Выясним, какой из факторов в наибольшей степени ответственен за мультиколлинеарность. Для этого определим коэффициент детерминации, выделяя каждый фактор в качестве зависимой переменной:
А) 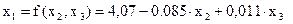 ,
,
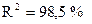 ;
;
Б) 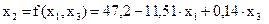 ,
,
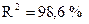 ;
;
В) 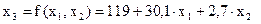 ,
,
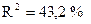 .
.
Таким образом, мультиколлинеарность вносится 1 и 2 признаками в равной степени и в меньшей степени – третьим признаком. Однако отбросить первый и второй признаки в данном случае нельзя.
Применим метод главных компонент.
Решение задачи в программе STATGRAPHICS
Special-Multyvariative methods – Principal Components
| Component number | Eigenvalue (l) | Percent of variance | Cumulative Percentage | |
| 1,9303 | 64,344 | 64,344 | Это матрица собствен. значений L | |
| 1,0356 | 34,521 | 98,865 | ||
| 0,0340 | 1,135 |
Т. е. 98,865 % общей дисперсии содержится в двух первых компонентах х. Следовательно, третья компонента может быть отброшена.
Component Weights
| Главные компоненты | |||
| Признаки | f1 | f2 | |
| X1 | -0,095 | 0,97 | |
| X2 | -0,696 | -0,215 | |
| X3 | -0,711 | 0,08 |
Это матрица факторных нагрузок А. Из нее видно, что главная компонента 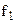 связана с
связана с 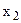 и
и 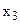 , а компонента
, а компонента 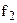 - связана с
- связана с 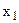 .
.
Data Table
| Row | Component 1 | Component 2 |
| 0,156245 | 1,18691 | |
| 0,532782 | 0,690533 | |
| -1,48884 | 0,487154 | |
| 2,24722 | -0,22817 | |
| -1,44105 | -0,46866 | |
| -0,00636 | 1,66866 |
Коэффициент корреляции между 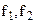 :
:
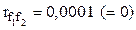 , таким образом, три признака преобразованы в 2 главные компоненты, не коррелированные между собой.
, таким образом, три признака преобразованы в 2 главные компоненты, не коррелированные между собой.
Рассмотрим более простой пример.
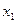
| 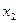
|
Переменные полностью коррелированы, 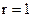 .
.
Матрица собственных значений:
Матрица парных коэффициентов корреляции

Из уравнения 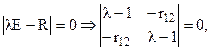 получим
получим
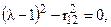 обозначим
обозначим 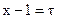 .
.
Получим: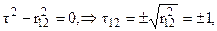 т. е.
т. е.
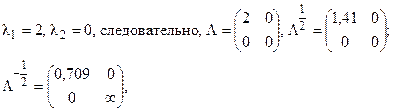
т. е. вся дисперсия в первой компоненте.
| <== предыдущая страница | | | следующая страница ==> |
| Компонентный анализ | | | Матрицы главных компонент |
Дата добавления: 2014-03-19; просмотров: 349; Нарушение авторских прав

Мы поможем в написании ваших работ!