Жидкостная экстракция

ЭКСТРАКЦИЯ.

Лекция 13

Экстракция – процесс извлечения одного или нескольких компонентов из растворов или твердых тел с помощью избирательных растворителей (экстрагентов). При взаимодействии с экстрагентом в нем хорошо растворяются только извлекаемые компоненты и значительно слабее или практически вовсе не растворяются остальные компоненты исходной смеси. Экстракцию из твердых тел жидкостью (растворителем) называют экстрагированием. Если в этом процессе в качестве растворителя используется вода, то такой процесс называется выщелачиванием. В химической технологии экстракция из растворов экстрагентами более распространена, чем экстракция из твердых тел.

Процессы жидкостной экстракции применяются в химической, нефтехимической, фармацевтической, гидрометаллургической и других отраслях промышленности получении редких и рассеянных элементов из растворов. Жидкостная экстракция, наряду с перегонкой, является одним из основных методов разделения однородных жидких смесей. Процесс экстракции обычно экономически выгоднее ректификации, поскольку при экстракции не нужно испарять всю жидкую смесь. Обычно жидкостную экстракцию с сочетают с ректификацией, которую применяют для регенерации экстрагента. Экстракт – раствор извлеченных веществ в экстрагенте, рафинат – остаточный исходный раствор.

На рис. 4.1 представлена схема без регенерации. Чаще всего используются схемы с регенерацией экстрагента. Исходный раствор 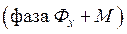и экстрагент подается в экстракционный аппарат – экстрактор, в котором происходит перенос вещества М из фазы 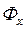в фазу 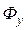. В результате, получают экстракт 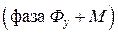и рафинат .

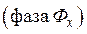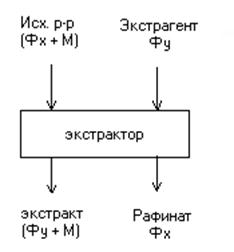
Рис. 4.1. Схема проведения экстракции.

4.1.1 Равновесия в системе жидкость – жидкость.

Для трехкомпонентной системы жидкость – распределяемое вещество–жидкость 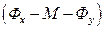можно изменять концентрацию одной из фаз без нарушения равновесия. По правилу фаз Гиббса:

В процессе жидкостной экстракции обычно Т не меняется, Р на равновесие системы не влияет. По этому для экстракции .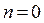

Данной концентрации распределяемого вещества х в одной фазе в состоянии равновесия соответствует определенная концентрация 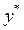вещества в другой фазе. Эта связь соответствует закону распределения: отношение равновесных концентраций распределяемого между двумя жидкими фазами вещества при Т=const есть величина постоянная:

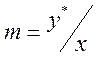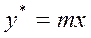или (4.1)

где у* и х – равновесные концентрации распределяемого вещества соответственно в экстракте и рафинате, m – коэффициент распределения.

По формуле (4.1) линия равновесия должна быть прямой, выходящей из начала координат. Однако это справедливо для случая полной взаимной нерастворимости участвующих в процессе фаз, что довольно редко встречается в реальных условиях.

Обычно m зависит от концентрации распределяемого вещества при Т=const, если же меняется и Т, то величина m может меняться еще сильнее.

Линии равновесия на диаграмме у-х при постоянной температуре называют изотермами экстракции (рис. 4.2). Если известны изотермы для разных Т, то становится возможным выбрать наиболее приемлемое Т.

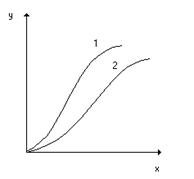
Рис.4.2. Типичные изотермы экстракции неэлектролитов (1) и электролитов (2).

Треугольные диаграммы. Составы тройных смесей в состоянии равновесия удобно изображать в треугольной диаграмме Гиббса. Отметим, что часто фазы, участвующие в процессе экстракции, частично растворимы друг в друге. Тогда экстракт помимо экстрагента и растворенного вещества содержит еще некоторое количество растворителя из исходного раствора, а рафинат помимо первоначального раствора и некоторого количества растворенного вещества – определенное количество экстрагента. Оба раствора состоят из трех компонентов.

А, В, С – чистые компоненты.

В точке А – чистый Фх,

в точке В – чистый М,

в точке С – чистый Фу.

Точки на площади треугольника соответствуют составам трехкомпонентных растворов.

Определим концентрации компонентов в точке М. Для этого через точку М проведем параллельные линии к линиям АВ, ВС и АС до пересечения. При этом отрезок 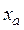определяет концентрацию компонент А в точке М, 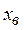– компонента В, 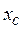– компонента С.

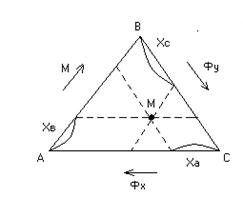
Рис. 4.3. Треугольная диаграмма.

С помощью треугольных диаграмм, используя правила рычага, можно достаточно просто определить не только состав, но и количество (массу) фаз (рис.4.4).

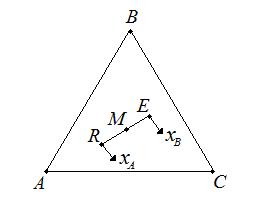
Рис.4.4. Правила рычага на треугольной диаграмме.

Средний состав смеси, образующихся при смешении двух трехкомпонентных смесей (например, состава R и E) лежит на отрезке прямой, соединяющей эти точки (например, состава М). Эта точка М по правилу рычага разделяет отрезок на отрезки, обратно пропорциональные количествам (массам) исходных смесей. При разделении М кг смеси 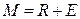по правилу рычага имеем:

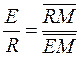(4.2)

где R и E – количества рафината и экстракта соответственно, кг. Выражение (4.2) позволяет найти положение точки М, если известны количества растворов R и E.

Кривая равновесия

При расчете процесса экстракции, как и для любого массообменного процесса, необходимо знание равновесных концентраций.

Рассмотрим кривую равновесия в треугольной диаграмме.

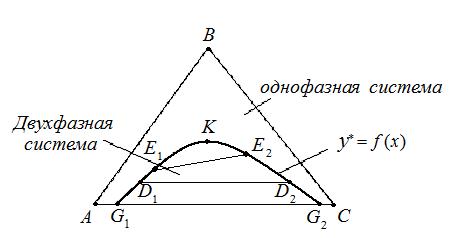
Рис. 4.5. Равновесная кривая в треугольной диаграмме.

А – 100% - растворитель в исходном растворе, В – 100% - растворенное вещество, С – 100% - экстрагент.

Линии АВ, ВС, СА – характеризуют состав двухкомпонентных растворов. Пусть А и В, В и С, неограниченно растворимы друг в друге,

а А и С – ограниченно растворимы.

На участке G₁ и G₂ любая смесь компонентов А и С расслаивается на два однородных двухкомпонентных раствора, состава которых отвечают точкам G₁ и G₂ . Если к ним добавить В, получим трехкомпонентный расслаивающий раствор соответствующий точкам D₁ и D₂. Хорда соединяющие точки D₁ и D₂ соответствует растворам, находящихся в равновесии друг с другом. При дальнейшим добавлении компонента В получим расслаивающиеся системы характеризующиеся точкам Е₁ и Е₂ и т.д. Эти точки постепенно сближаются, наконец соединятся в точке К. Точка К– критическая точка, соответствует однофазному раствору.

Соединяя точки G₁ , D₁ , Е₁ , … , G₂ , D₂ , Е₂ и т.д. получают равновесную (бинодальную) кривую, выше которой система однофазна и для процесса экстракции интереса не представляет.

Хорды, соединяющие точки D₁ и D₂ , E₁ и E₂ и т.д. на бинодальной кривой, называют конодами, которые непараллельны друг другу, так как компонент В неравномерно распределяется между компонентами А и С. Любая точка, лежащая на площади, ограниченной равновесной кривой кривой, соответствует двухфазной системе

Взаимная растворимость с увеличением температуры повышается, поэтому область существования гетерогенных систем уменьшается. При высоких температурах может вообще исчезнуть (точка Т_кр на рис. 4.6).

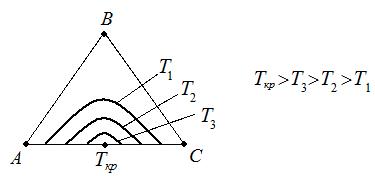
Рис. 4.6. Влияние Т на равновесную кривую.

Селективность экстрагента. Основным свойством экстрагента является селективность, которая характеризует его способность преимущественно извлекать один из двух, трех и более компонентов раствора. Селективность С по отношению к В выражается отношением концентраций компонентов В и А в фазе экстракта 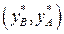, разделенным на отношение концентраций в фазе рафината 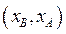. Селективность экстрагирования по отношению к распределяемому компоненту характеризуется коэффициентом селективности (коэффициент разделения) :

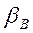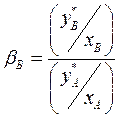(4.3)

или с учетом (4.1)

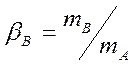(4.4)

Как видно, чем больше 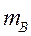тем больше 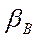. Если 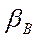=1, то селективность равна 0. В реальных условиях 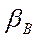больше 2. Увеличение 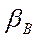можно добиться изменением рН раствора.

4.1.2 Материальный баланс процесса жидкостной экстракции.

Однократная (одноступенчатая) экстракция.

Рассмотрим одноступенчатую (однократную) экстракцию. Этот простейший метод заключается в том, что исходный раствор F и экстрагент S перемешивается в смесителе, после чего разделяется на два слоя: экстракт E и рафинат R:

F + S = E + R (4.5)

Здесь F,S – количество исходного раствора и экстрагента соответственно кг.

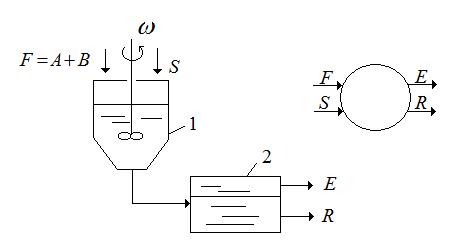
Рис. 4.7 Схема одноступенчатой экстракции: 1 – смеситель, 2 – отстойник (сепаратор).

Фазы, участвующие в жидкостной экстракции, обладают частичной взаимной растворимостью. Тогда система как минимум является трехкомпонентной. Для трехкомпонентной смеси используется треугольная диаграмма. Уравнение (4.5) можно переписать как:

F + S = N = R + E (4.6)

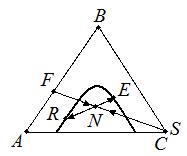
Рис. 4.8. К выводу уравнения материального баланса.

Выражение (4.6) позволяет представить материальный баланс на треугольной диаграмме как процесс смешения потоков F + S = N и затем разделения этой тройной смеси состава N на потоки R + E. По правилу рычага можно записать:

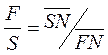(4.7)

Тогда при заданной F находим необходимое значение S для процесса. Соотношение потоков Е и R находят по формуле

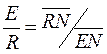(4.8)

Материальный баланс компонентов А и В в потоках экстракта Е и рафината R с учетом рис.4.3 имеет вид:

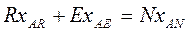
(4.9)

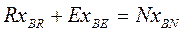
Так как сумма концентраций всех трех компонентов А, В, С равна 100%, то матбаланс по компоненту С не нужен. Учитывая, что N = E + R получим:

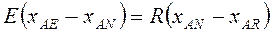
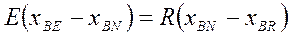
Разделив одно на другое получим:

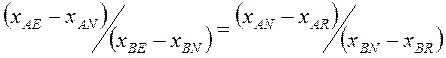(4.10)

Уравнение (4.10) является уравнением прямой линии. По уравнениям (4.7) – (4.10) можно найти состав любого потока, если известны количества и состав трех остальных потоков.

4.1.3 Кинетика жидкостной экстракции.

Поскольку при экстракции

- массообмен происходит между двумя жидкими фазами,

- для развития поверхности фазового контакта обычно одну из жидкостей диспергируют.

- 1. распределяемое вещество В переходит из сплошной фазы к поверхности капли и затем внутрь ее

- 2. или (наоборот) из капли через поверхность раздела фаз в ядро потока сплошной фазы.

В соответствии с общим уравнением массопередачи количество проходящего из одной фазы в другую вещества можно записать:

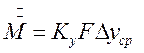(4.11)

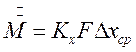
(4.12)

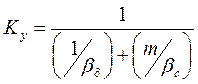(4.13)

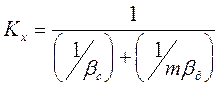(4.14)

Здесь 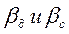- коэффициенты массоотдачи для дисперсной фазы и сплошной фазы.

Поскольку поверхностью контакта фаз при экстракции являются капли, то массоперенос осуществляется через сферическую поверхность. Очевидно, что гидродинамические условия внутри капли и в сплошной фазе различны. Поэтому массоперенос в пределах каждой из фаз не может быть описан идентичным уравнением. Рассмотрим частные случаи.

Случай первый – диффузионное сопротивление внутри капли незначительное по сравнение диффузионным сопротивлением в сплошной фазе, тогда 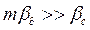, следовательно 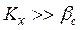. Коэффициент массоотдачи 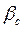может быть определен по критериальному уравнению:

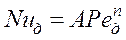(4.15)

Случай второй – диффузионное сопротивление внутри капли велико, в то время как диффузионное сопротивление сплошной фазы незначительно, тогда 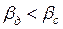. В этом случае 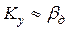. Коэффициент массотдачи 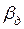определяется по аналогичному уравнению (4.15).

Случай третий – диффузионные сопротивления сплошной фазы и внутри капли примерно равны. В этом случае необходимо использовать уравнения (4.11) и (4.13) или (4.12) и (4.14).

4.1.3 Основные способы проведения жидкостной экстракции.

Однократная (одноступенчатая) экстракция.

Простейшим способом проведения процесса экстракции является одноступенчатая экстракция (рис.4.7). Исходная смесь и экстрагент вводятся в смеситель 1, где происходит диспергирование и процесс массопередачи, а затем переходит в сепаратор 2, в котором разделяются на две фазы: рафинат и экстракт. Процесс может проводиться как непрерывно, так и периодически. Структура потоков в смесителе близка к МИС и выходящие из аппарата фазы экстракта и рафината находится в состоянии равновесия.

Многоступенчатая экстракция с перекрестным током растворителя.

Исходный раствор и соответствующие рафинаты обрабатывают порцией свежего экстрагента 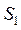и 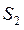и т. д. На каждой ступени экстракции, состоящей из смесителя и отстойника, причем рафинаты направляют последовательно в следующие ступени , а экстракты 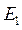и 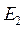и т. д. после каждой ступени выходят из колонны.

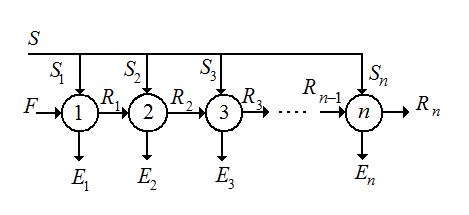
Рис. 4.9 Схема многократной экстракции с противоточным током растворителя (1,2 … n – ступени).

По этому способу можно полностью извлечь из исходного раствора распределяемый компонент и получить чистый рафинат. Однако, неизбежны потери растворителя, содержащегося в исходном растворе, так как в каждой ступени происходит частичное удаление растворителя экстрактом.

Многократная экстракция с противоточным движением растворителя.

Этот способ проведения экстрагирования характеризуется многократным контактированием в ступенях 1, 2 и т. д. при противоточном движении потоков рафината R и экстракта Е при условии подачи исходного раствора F и и экстагента S с противоположных концов.

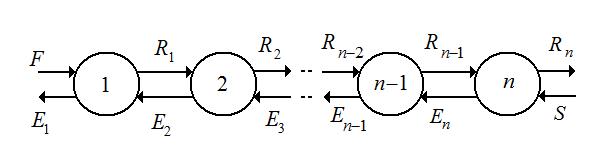
Рис. 4.10 Схема многократной экстракции с противоточным движением растворителя (1,2 … n – ступени).

Можно получить продукты заданного свойства при высокой производительности установки.

Непрерывная противоточная экстракция.

Такой способ экстрагирования осуществляют в аппаратах колонного типа (например, насадочных). Более тяжелый раствор поступает сверху, а в нижнюю часть колонны поступает легкая фаза (рис.4.11).

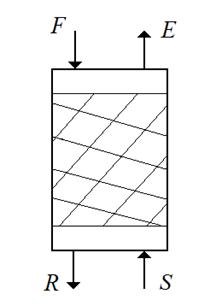
Рис.4.11. Схема непрерывной противоточной экстракции.

При непрерывной противоточной экстракции фазы взаимодействуют друг с другом не достигая равновесия. Противоточное движение фаз при экстракции обеспечивает большую степень извлечения распределенного компонента В, чем прямоточное.

Дата добавления: 2014-03-22; просмотров: 1363; Нарушение авторских прав

Мы поможем в написании ваших работ!