Выборочная сумма

Иногда необходимо суммировать не весь диапазон, а только ячейки, отвечающие некоторым условиям (критериям). В этом случае используют функцию СУММЕСЛИ.

Синтаксис функции

СУММЕСЛИ(А;В;С),

где А - диапазон вычисляемых ячеек.

В - критерий в форме числа, выражения или текста, определяющего суммируемые ячейки;

С - фактические ячейки для суммирования.

В тех случаях, когда диапазон вычисляемых ячеек и диапазон фактических ячеек для суммирования совпадают, аргумент С можно не указывать.

Можно суммировать значения, отвечающие заданному условию. Например, в таблице на рис.7.2 суммированы только студенты по странам, при условии, что число студентов от страны превышает 200.

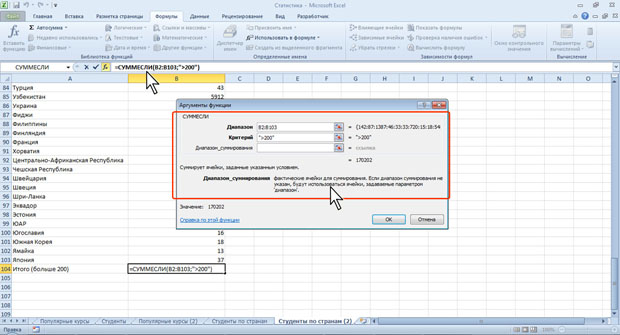
Рис. 7.2. Выборочное суммирование

Можно суммировать значения, относящиеся к определенным значениям в смежных ячейках. Например, в таблице на рис.7.3 суммированы только студенты, изучающие курсы со средней оценкой выше 4,1. Критерий можно ввести с клавиатуры или выбрать нужную ячейку на листе.

Рис. 7.3. Выборочное суммирование

Дата добавления: 2014-02-26; просмотров: 404; Нарушение авторских прав

Мы поможем в написании ваших работ!