
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Кинематические элементы движущейся жидкости
Основной кинематической характеристикой гидродинамического поля является линия тока - кривая, в каждой точке которой вектор скорости направлен по касательной к кривой. И ходя из данного определения можно записать дифференциальное уравнение линии  тока:
тока:
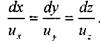
Если через некоторую неподвижную в пространстве кривую провести линии тока, то полученная поверхность называется поверхностью тока, а образованное этой поверхностью тело будет называться трубкой тока. Жидкость, наполняющая трубку тока, называется элементарной струйкой. Поскольку линии тока никогда не пересекаются, то поверхность трубки тока является непроницаемой 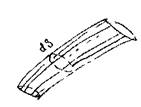 внешней границей для элементарной струйки жидкости. Сечение трубки тока, нормальное к линиям тока называется живым сечением элементарной струйки dS. При установившемся движении жидкости понятия линии тока и траектории движения частицы жидкости совпадают. Объём жидкости протекающий через живое
внешней границей для элементарной струйки жидкости. Сечение трубки тока, нормальное к линиям тока называется живым сечением элементарной струйки dS. При установившемся движении жидкости понятия линии тока и траектории движения частицы жидкости совпадают. Объём жидкости протекающий через живое
сечение элементарной струйки в единицу времени называется расходом элементарной струйки.
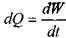 ?
?
где: 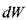 объём жидкости, протекающий через живое сечение трубки тока за
объём жидкости, протекающий через живое сечение трубки тока за
время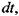
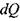 расход жидкости в живом сечении трубки тока. Размерность расхода жидкости в системе СИ -м/с.
расход жидкости в живом сечении трубки тока. Размерность расхода жидкости в системе СИ -м/с.
Гидродинамическое поле считается потенциальным (безвихревым), если в этом поле отсутствует вихревое движение жидкости. В потенциальном поле может существовать лишь поступательное или криволинейное движение жидкости. 3.3 Уравнение неразрывности жидкости
Если в гидродинамическом поле отсутствуют вихри, то; для такого поля можно записать уравнение, связывающее параметры движущейся жидкости (плотность жидкости) с
параметрами, характеризующими условия движения жидкости. Вывод такого уравнения основан на представлении жидкости как сплошной непрерывной среды, в силу чего такое уравнение получило название уравнения неразрывности.
Для этой цели выделим в пространстве малый элемент жидкой среды в виде па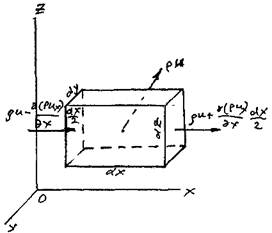 раллелепипеда, стороны которого будут равны соответственно.
раллелепипеда, стороны которого будут равны соответственно.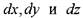 . Грани
. Грани
параллелепипеда пусть будут параллельны координатным плоскостям. В центре элемента в данный момент времени будет находиться частица жидкости, плотность которой равна р, а вектор скорости движения и направлен таким образом, что жидкость втекает внутрь элемента через левую, нижнюю и переднюю грани элемента и вытекает через противоположные грани. Будем считать также, что размер элемента достаточно мал, и можно допустить, что в пределах этого элемента изменение плотности жидкости и скорости её движения будет прямо пропорционально расстоянию от центра элемента. Одновременно размеры граней будут достаточно велики по сравнению с точкой, что позволит утверждать, что плотность жидкости и скорость во всех точках граней будут одинаковыми, как и плотность жидкости в пределах соответствующих граней. Тогда произведение плотности жидкости на вектор скорости (импульс) в специальной литературе часто называют вектором
массовой скорости ри.
В таком случае проекция вектора массовой скорости в центре левой грани элемента на ось ОХ будет равна:
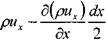
а проекция вектора массовой скорости в центре правой грани элемента на ось ОХ:
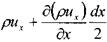 &
&
Масса жидкости, поступившая через левую грань элемента за малый интервал времени dt\
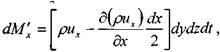
масса жидкости, вытекшая через правую грань элемента за малый интервал времени dt:
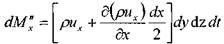
Изменение массы жидкости внутри элемента при движении жидкости вдоль оси ОХ:
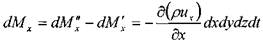
Аналогично, изменение массы жидкости внутри элемента при движении жидкости вдоль оси OY: 1,
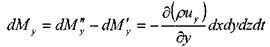
и вдоль оси OZ:
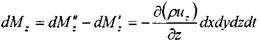
Окончательно, изменение массы жидкости внутри элемента при движении жидкости в произвольном направлении:
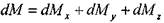 ? или
? или
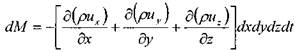
Величина плотности жидкости в начальный момент (до начала движения жидкости t = Q) - р, а по истечении бесконечно малого интервала времени (т.е.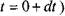
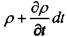
Масса жидкости в объёме выделенного элемента в начальный момент времени:
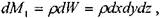
для времени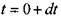 :
:
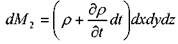
Изменение массы жидкости за бесконечно малый интервал времени dt:
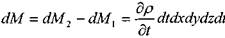 •> или:
•> или:
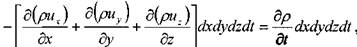 i
i
откуда для наиболее общего случая нестационарного поля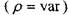 дифференциальное
дифференциальное
уравнение неразрывности запишется в следующем виде:
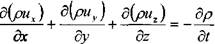
и для частного случая - стационарного поля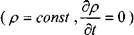 :
:
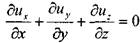 «
«
В векторной форме уравнения неразрывности жидкости запишутся в следующем виде:
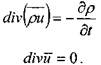 ?
?
| <== предыдущая страница | | | следующая страница ==> |
| Сообщающиеся сосуды | | | Уравнение неразрывности для элементарной струйки жидкости |
Дата добавления: 2014-02-26; просмотров: 319; Нарушение авторских прав

Мы поможем в написании ваших работ!