А. Тетрагональная сингония

Формулы и виды симметрии:

1) L₄4L₂5PC – планаксиальный вид симметрии;

2) L₄4L₂ – аксиальный;

3) L₄4P – планальный;

4) L₄PC – центральный;

5) L₄ – примитивный;

6) L_i42L₂2P – инверсионно-планальный;

7) L_i4 – инверсионно-примитивный.

При нахождении в кристаллах L_i4 рекомендуется руководствоваться дополнительным признаком: ось L_i4 проявляет себя как обычная ось L₂, но она перпендикулярна квадратному сечению кристалла.

Простые формы (рис. 3.1-3.27):

1) моноэдр (рис.3.1);

2) пинакоид (рис.3.2);

3)тетрагональная призма – 4 грани, параллельные одному направлению (поперечное сечение – квадрат) (рис. 3.3);

4) дитетрагональная призма – 8 граней, параллельных одному направлению (поперечное сечение – дитетрагон) (рис.3.6);

5) тетрагональная пирамида – 4 грани, пересекающиеся в одной точке (поперечное сечение – квадрат) (рис.3.9);

6) дитетрагональная пирамида – 8 граней, пересекающихся в одной точке (поперечное сечение – дитетрагон) (рис.3.12);

7) тетрагональная дипирамида – 8 граней, состоит как бы из двух равных тетрагональных пирамид (поперечное сечение – дитетрагон) (рис.3.15);

8) дитетрагональная дипирамида – 16 граней, состоит как бы из двух равных дитетрагональных пирамид (поперечное сечение – дитетрагон) (рис.3.18);

9) тетрагональный трапецоэдр (трапеца – четырёхугольник с двумя равными соседними сторонами) – имеет 8 граней; напоминает дипирамиду, одна половина которой сдвинута относительно другой на некоторый угол, присутствует только в аксиальном виде симметрии(L₄ 4L₄) (рис.3.21);

10) тетрагональный тетраэдр – отличается от ромбического тем, что имеет поперечное сечение через центр в форме квадрата, перпендикулярно этому сечению проходит ось Li₄ (рис.3.25);

11) тетрагональный скаленоэдр (скаленос – косоугольный треугольник) – имеет 8 граней, представляет собой как бы удвоенный тетраэдр (поперечное сечение – дитетрагон, перпендикулярно ему проходит ось Li₄) (рис.3.26).

Б.Тригональная сингония

Формулы и виды симметрии:

1) L₃ 3L₂ 3PC – планальный вид симметрии;

2) L₃ 3L₂ – аксиальный;

3) L₃ 3P – планальный;

4) L₃C – центральный;

5) L₃ – примитивный.

В.Гексагональная сингония

Формулы и виды симметрии:

1) L₆ 6L₂ 7PC – планальный вид симметрии;

2) L₆ 6L₂ – аксиальный;

3) L₆ 6P – планальный;

4) L ₆PC – центральный;

5) L₆ – примитивный;

6) Li₆ (L₃P) – инверсионно-примитивный;

7) Li₆3L₂3P (L₆3L₂4P) – инверсионно-планальный.

Тригональная и гексагональная сингонии имеют общие простые формы и поэтому рассматриваются далее совместно.

Простые формы (рис.3.1-3.27):

1) моноэдр (рис.3.1);

2) пинакоид (рис.3.2);

3-6) призмы: тригональные, дитригональные, гексагональные, дигексагональные (формы поперечного сечения – тригон, дитригон, гексагон, дигексагон) (рис.3.4, 3.5, 3.7, 3.8);

7-10) пирамиды: тригональные, дитригональные, гексагональные, дигексагональные (формы поперечного сечения – тригон, дитригон, гексагон, дигексагон) (рис.3.10, 3.11, 3.14, 3.15);

11-14) дипирамиды: тригональные, дитригональные, гексагональные, дигексагональные (формы поперечного сечения – тригон, дитригон, гексагон, дигексагон) (рис.3.13, 3.14, 3.19, 3.20);

15) ромбоэдр – имеет 6 граней в форме ромбов, каждая верхняя грань расположена симметрично относительно двух нижних и наоборот (рис.3.24);

16) дитригональный скаленоэдр – имеет 12 граней, представляет собой как бы удвоенный ромбоэдр, пара двух верхних граней располагается симметрично относительно двух пар нижних граней (рис.3.27);

17-18) трапецоэдры: тригональный и гексагональный, имеют соответственно 6 и 12 граней, аналогично тетрагональному трапецоэдру, верхняя грань в трапецоэдре сдвинута относительно нижней на некоторый угол (рис.3.22, 3.23).

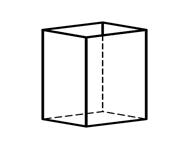
3.1 3.2 3.3

Моноэдр Пинакоид Тетрагональная призма

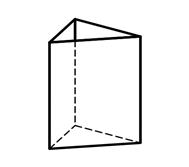
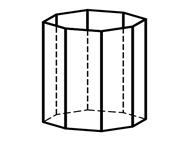
3.4 3.5 3.6

Тригональная призма Гексагональная призма Дитетрагональная призма

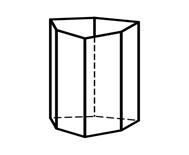
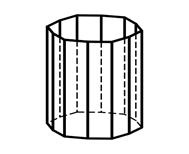
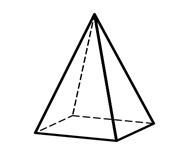
3.7 3.8 3.9

Дитригональная Дигексагональная Тетрагональная

призма призма пирамида

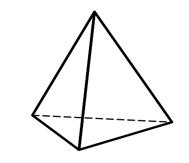
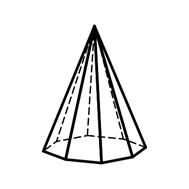
3.10 3.11 3.12

Тригональная Гексагональная Дитетрагональная

пирамида пирамида пирамида

Рис. 3. Простые формы средней категории сингоний

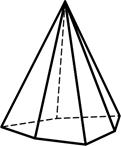
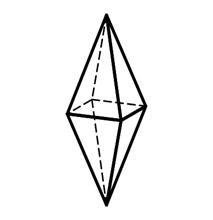
3.13 3.14 3.15

Дитригональная Дигексагональная Тетрагональная

пирамида пирамида дипирамида

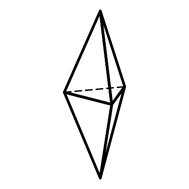
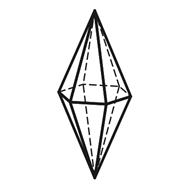
3.16 3.17 3.18

Тригональная Гексагональная Дитетрагональная

дипирамида дипирамида дипирамида

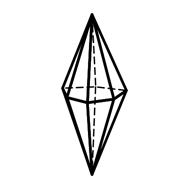
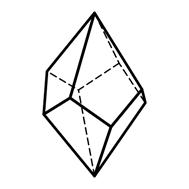
3.19 3.20 3.21

Дитригональная Дигексагональная Тетрагональный

дипирамида дипирамида трапецоэдр

Рис. 3. Простые формы средней категории сингоний (продолжение)

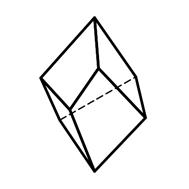
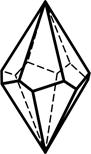
3.22 3.23 3.24

Тригональный Гексагональный Ромбоэдр

трапецоэдр трапецоэдр

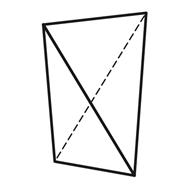
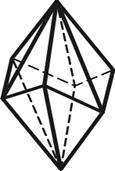
3.25 3.26 3.27

Тетрагональный Тетрагональный Дитригональный

тетраэдр скаленоэдр скаленоэдр

Рис. 3. Простые формы средней категории сингоний (окончание)

1.9. Высшая категория сингоний

Кубическая сингония

Формулы и виды симметрии:

1) 3L₄ 4L₃ 6L₂ 9PC – планальный вид симметрии;

2) 3L₄ 4L₃ 6L₂ – аксиальный;

3) 4L₃ 6L₂ 6P – планальный;

4) 4L₃ 3L₂ 3PC – центральный;

5) 4L₃ 3L₂ – примитивный.

Простые формы: в кубической сингонии существует 5 основных простых форм и 10 производных.

Основные простые формы(рис.4.1-4.15):

1) кубический тетраэдр – 4 равные грани в форме правильного треугольника, из которого каждые 3 грани пересекаются в одной точке (рис.4.1);

2) октаэдр – 8 граней в форме правильных треугольников (рис.4.2);

3) гексаэдр (куб) – 6 граней в форме квадратов (рис.4.3);

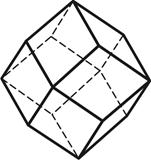
4) ромбо-додекаэдр – 12 граней в форме ромбов (рис.4.4);

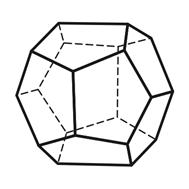
5) пентагон-додекаэдр – 12 граней в форме пятиугольников (рис.4.5).

Производные простые формы:

из кубического тетраэдра образуются следующие производные:

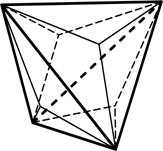
6) тригон-тритетраэдр – состоит из 12 граней в форме равнобедренных треугольников, образуется путём расщепления каждой грани тетраэдра на 3 треугольные грани следующим образом (рис.4.6);

7) тетрагон-тритетраэдр – 12 граней в форме четырёхугольников, образуется посредством утроения каждой грани тетраэдра следующим образом (рис.4.7);

8) пентагон-тритетраэдр – 12 граней в форме пятиугольников (рис. 4.8);

9) гексатетраэдр – 24 грани в форме треугольников, образуется посредством ушестерения каждой грани тетраэдра (рис.4.9).

Все производные от тетраэдра в первом приближении похожи на тетраэдр.

Из октаэдра аналогичным способом образуются следующие производные:

10) тригон-триоктаэдр – 24 грани в форме равнобедренных треугольников (рис.4.10);

11) тетрагон-триоктаэдр – 24 грани в форме четырёхугольников (рис.4.11);

12) пентагон-триоктаэдр – 24 грани в форме пятиугольников (рис.4.12);

13) гексоктаэдр – 48 граней в форме разносторонних треугольников (самая большая простая форма по количеству граней) (рис.4.13);

Из гексаэдра образуется одна производная форма:

14) тетрагексаэдр – 24 грани в форме равнобедренных треугольников, образуется посредством учетверения каждой грани гексаэдра (рис.4.14).

Из пентагон-додекэдра образуется одна производная:

15) дидодекаэдр – 24 грани в форме четырёхугольников, образуется посредством удвоения каждой грани пентагон-додекаэдра (рис.4.15).

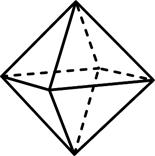
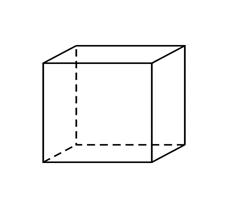
4.1 4.2 4.3

Тетраэдр Октаэдр Гексаэдр (куб)

4.4 4.5 4.6

Ромбо-додекаэдр Пентагон-додекаэдр Тригон-тритетраэдр

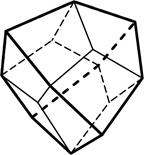
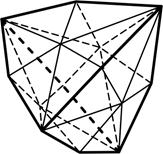
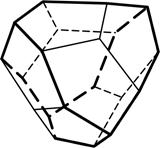
4.7 4.8 4.9

Тетрагон-тритетраэдр Гексатетраэдр Пентагон-тритетраэдр

Рис. 4. Простые формы кубической сингонии

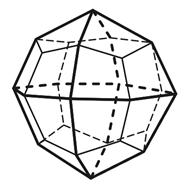
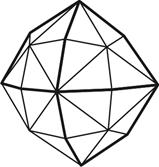
4.10 4.11 4.12

Тригон-триоктаэдр Тетрагон-триоктаэдр Гексоктаэдр

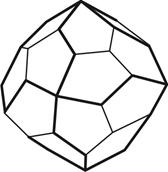
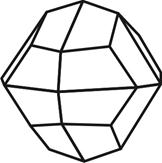
4.13 4.14 4.15

Пентагон-триоктаэдр Тетрагексаэдр Дидодекаэдр

Рис. 4. Простые формы высшей категории сингонии (окончание)

Принцип наименованияпростых форм кубической сингонии заключается в следующем. В сложных названиях первое слово означает форму грани (тригон – треугольник, тетрагон – четырёхугольник, пентагон – пятиугольник)\. Второе слово – количество граней в простой форме.

При указании количества граней используют следующие греческие числительные:

ди – 2; три – 3; тетра – 4; гекса – 6; окта – 8; додека – 12,

при этом 12-гранники называются по разному: додекаэдр и тритетраэдр (три – 3, тетра – 4, 3Х4 = 12). Различие в том, что тритетраэдр является производной формой и корень этого слова даёт указание, из какой основной формы она образована (из тетраэдра). Поэтому 24-гранники называются также неодинаково: триоктаэдр, гексатетрадр, дидодекаэдр, тетрагексаэдр.

Все 15 простых форм кубической сингонии являются закрытыми.

Дата добавления: 2014-09-10; просмотров: 2496; Нарушение авторских прав

Мы поможем в написании ваших работ!