
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Омск – 2007
Рекомендовано к изданию ученым советом физического факультета от 26 декабря 2006 года.
Механика: Лабораторный практикум. ч. 2. (для студентов физического факультета) / Сост.: Сычёв С.А., Серопян Г.М., Скутин А.А., Югай К.Н., Муравьев А.Б.
Практикум включает 4 лабораторные работы. Материал соответствует Государственному образовательному стандарту по специальности «Физика». Может быть использован студентами других специальностей.
Лабораторная работа № 5
Изучение законов гармонического движения
на примере физического и математического маятников.
Цель работы: Научиться определять ускорение свободного падения с помощью математического и физического маятников.
Приборы и принадлежности: физический маятник (оборотный маятник), математический маятник (маятник Бесселя), секундомер, призма, линейка или рулетка, отвертка.
 |
 О1
О1
 | |||
| |||

 Р1
Р1

 l1
l1
 |


 C
C
 | ||
 |

 l2
l2



 М
М


 O2
O2
 | ||||
 | ||||
 | ||||


 P2
P2
Рис. 1. Физический маятник. Рис. 2. Маятник Бесселя.
Упражнение 1.
Физический маятник, используемый в данной работе (рис. 1), состоит из металлического стержня с закрепленными на нем опорными призмами О1 и О2 и грузами m1 и m2, которые могут перемещаться вдоль стержня. Перемещение грузов вдоль стержня изменяет момент инерции маятника и положение центра масс, и период его колебаний.
Применение оборотного маятника основано на свойстве сопряженности точки подвеса (О1) и центра качания (О2). Центром качания физического маятника называется точка, удаленная от оси вращения по линии, проходящей через точку подвеса О1 и центр масс С, на расстояние, равное приведенной длине маятника 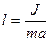 , где J – момент инерции маятника, m – его масса,
, где J – момент инерции маятника, m – его масса, 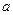 – расстояние от точки подвеса до центра масс.
– расстояние от точки подвеса до центра масс.
Пусть момент инерции физического маятника относительно точки подвеса равен J. Тогда для полной механической энергии колебаний имеем:
J 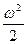 + mg
+ mg 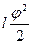 = const, (1)
= const, (1)
где первое слагаемое – это кинетическая энергия, а второе – потенциальная.

Рис. 3.
Потенциальная энергия маятника при колебаниях достигает максимального значения mgh, когда кинетическая становится равной нулю и достигает нулевого значения, когда кинетическая энергия максимальна. Пусть центр масс физического маятника в процессе гармонического колебания поднимается на высоту h (рис. 3). Тогда выразим эту высоту через угол отклонения 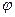 :
:
h = 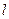 -
-  cos
cos 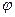 =
= 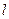 (1 – cos
(1 – cos 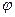 ) = 2
) = 2 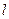 sin2
sin2 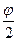 ≈
≈ 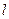
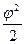 , (2)
, (2)
где sin 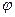 ≈
≈ 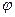 для малых углов отклонения.
для малых углов отклонения.
При выводе формулы (2) использовано известное тригонометрическое тождество:
sin2 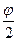 =
= 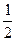 (1 – cos
(1 – cos 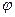 ) . (3)
) . (3)
 Угловая скорость
Угловая скорость 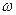 =
= 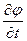 =
= 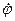 и тогда уравнение (1) запишется:
и тогда уравнение (1) запишется:
J 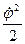 + mg
+ mg 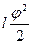 = const .
= const . 
 (4)
(4)
Произведя дифференцирование (4) по времени, получим:
J 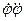 + mg
+ mg 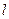
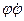 = 0. (5)
= 0. (5)
Уравнение (5) можно переписать как
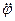 + mg
+ mg 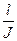
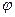 = 0 (6)
= 0 (6)
или
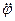 +
+ 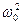
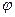 = 0, (6а)
= 0, (6а)
где 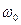 - частота собственных колебаний маятника.
- частота собственных колебаний маятника.
Из вида (6) получим для частоты собственных колебаний:
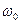 =
= 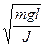 . (7)
. (7)
Для периода колебаний:
T = 2 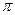
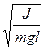 . (8)
. (8)
Для математического маятника J = m 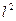 , поэтому
, поэтому

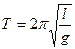 . (9)
. (9)
Поскольку на практике очень трудно добиться полного равенства периодов колебаний оборотного маятника при подвешивании его на верхнюю и нижнюю призмы, можно получить выражение для ускорения свободного падения в случае, когда периоды колебаний различаются:
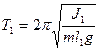 , (10)
, (10)
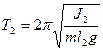 , (11)
, (11)
где g – ускорение свободного падения; J1 и J2 – моменты инерции маятника относительно осей 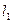 и
и 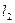 , равные по теореме Штейнера:
, равные по теореме Штейнера:
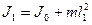 , (12)
, (12)
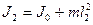 . (13)
. (13)
Здесь J0 – момент инерции маятника относительно оси, проходящей через центр масс; 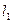 и
и 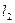 – соответственно расстояния от призм О1 и О2 до центра масс.
– соответственно расстояния от призм О1 и О2 до центра масс.
| <== предыдущая страница | | | следующая страница ==> |
| Лабораторная работа № 1. Задание 1. Разработать алгоритм сложения 8-разрядных двоичных целых чисел из табл | | | Выполнение измерений |
Дата добавления: 2014-11-08; просмотров: 224; Нарушение авторских прав

Мы поможем в написании ваших работ!